A journey of discovery? A death march? It’s the same thing!

This textbook is at the high school level, but it is written without the condescending tone typical of American high school textbooks. It is divided into two volumes, Geometry without Multiplication: White through Red Belt and Geometry with Multiplication: Blue and Black Belt. Our purpose is to instruct students in logic and rhetoric; thus, their arguments will be sound.

I rank high-school geometry students analogous to the way Tang–Soo–Do students are ranked. With these ranks and by addressing the student as Grasshopper, like in the old TV series Kung Fu (now on Nickelodeon), I hope to motivate students to strive for each successive colored belt. “A soldier will fight long and hard for a bit of colored ribbon,” quoth Napoleon Bonaparte.

White Belt	Foundations	Red Belt	Triangles, Advanced
Yellow Belt	Congruence	Blue Belt	Quadrature
Orange Belt	Parallelograms	Cho–Dan	Harmonic Division
Green Belt	Triangle Construction	Yi–Dan	Circle Inversion

The white-belt chapter teaches the geometry needed by all construction workers. Students learn how to make a foundation square with no auxiliary lines outside it. This is because it may be in a hole if it is for a basement, or it may be surrounded by trees or cliffs if a plot of land was cleared and graded for a house being built in a forest or cut into a hillside. Also, students learn how to construct strong and inexpensive wooden gantries and gates wide enough for farm equipment to go through. Bridges for both pedestrians and vehicles are described and the basics of fortresses are explained as a lead-in for the machine gun emplacement lessons to come. The yellow-belt chapter provides a theoretical foundation for the later chapters and concludes with geometry needed by architects for designing custom-made mansions, churches, museums, etc. The orange-belt chapter teaches geometry needed by asphalt men and the theory needed by architects. The green-belt chapter teaches geometry needed by sea captains and military officers. Many triangle construction problems are solved. There is detailed instruction on navigating a ship with a sextant and on setting ambushes with heavy machine guns. Students are trained for the International Mathematical Olympiad (IMO). Red belt presents theorems difficult enough that they went unsolved for decades and are now named after famous mathematicians. We consider the work of Miquel, Wallace, Torricelli, Napoleon, Fagnano, Euler, et. al. Students get serious about the IMO, though they cannot expect to win it until they become black belts.

Volume Two begins with the blue-belt chapter, which teaches the quadrature theory needed by surveyors to calculate the area of irregularly shaped farm fields. Multiplication is presented midway through and the power of the point is defined. We conclude with the Cramer-Castillon Problem, which my friend Milan Zlatanović found a much better solution to than Castillon did in 1776. Castillon had a lengthy and difficult solution that cites Menelaus’ Theorem, which is black belt geometry, while Zlatanović has a short and elegant solution that is mostly green belt, but it is delayed until blue belt because it cites the power of the point. After blue belt comes Cho–Dan (1st degree black belt), which is harmonic division. Yi–Dan (2nd degree black belt) is circle inversion and Sam–Dan (3rd degree black belt) is projective geometry. We conclude with an exam of problems taken from past International Mathematical Olympiad competitions. Volume One is for tradesmen, engineers and military officers; in Volume Two, we are all about the IMO!

The objective of Volume Two is to bring students up to the point where they can read books written for Olympians, such as The Geometry of Remarkable Elements by Constantin Mihalescu. Today, there is no English-language textbook that brings students up from entry-level to reading Mihalescu, which is Sam–Dan. College Geometry by Nathan Altshiller-Court is Cho–Dan.

A secondary objective of Geometry–Do, and particularly of the early chapters, is to oppose economists who hate deductive logic. The editor of the Real World Economics Review writes:

It is a completely mistaken idea that scientific theory is based on deductions from a series of postulates – that is the description of the methodology of mathematics… There is no science which uses axioms and logical deductions to derive scientific theory. Mathematics is not a “science” since it is not based in any direct way on observational evidence. Unlike scientific laws, mathematical laws are not affirmed observational evidence. Recognition of the possibility that there are bodies of knowledge which are not science would lead to greater tolerance and pluralism which is currently desperately needed.

Tolerance? No. Such outrageous talk by the World Economics Association has brought war and discord to our once quiet study of triangles. The editor of the Real World Economics Review is an influential man and he wields this terrifying power to no other end than to ban all mention of deductive logic. I was not the one who brought war to the study of geometry but, by teaching it as a martial art, I intend to win that war. Logic alone stands in the path of the WEA!

In 2000, the Post-Autistic Economics Network was founded; it denounced this author and every other mathematician involved in economics as “autistic.” In May 2011, they changed their name to the World Economics Association. The blacklisting of mathematicians had been going on for some time; Gerard Debreu renounced General Equilibrium in 1974 and blubbered an apology in 1983 at his Nobel awards ceremony, described as “Debreu’s axiomatic method” as though Debreu invented it and that he and it rise and fall together. But Alan Kirman describes a “palace revolution” in 1974 as mathematicians piled on and Debreu backpedaled. He quotes Debreu’s 1983 Nobel introduction, “Gerard Debreu symbolizes the use of a new mathematical apparatus,” but fails to point out how absurd this must have sounded to mathematicians who had ejected the man ten years earlier for bringing shame to a very old mathematical apparatus.

In 1974, the axiomatic method fell with such suddenness that oxygen masks deployed from the office ceilings of geometry teachers worldwide. In the year or two that it takes to replace high school textbooks, geometry was no longer taught as an axiomatic science. In 1987, when the U.S. stock market fell, economists – without any evidence – railed against deductive logic as the cause of economic collapse, a refrain that we would hear again in 2008; This is typical rhetoric: The failure of economics is due to the use of axiomatic method.

Today, 2016, I hope to bring geometry back to its axiomatic roots, as first employed by Euclid 2300 years past, while carefully distancing myself from that hated man, Gerard Debreu.

Postulate and axiom are synonymous, but I use the former term to refer to those stated by Euclid and the latter term to those added later regarding abstract algebra. Some geometers use these terms to distinguish Euclid’s controversial parallel postulate from his others, but I feel that, if we are going to teach Euclidean geometry, then we will refer to them all the same way. The work of Lobachevski, Bolyai and Riemann can exist peacefully alongside our work; consistency is not applicability. Also, I use the term axiom to refer to the foundation of other sciences such as Newton’s three axioms of motion, Euler’s three axioms of ballistics, Richardson’s seven axioms of meteorology, Einstein’s two axioms of relativity, or my own three axioms of economics.

But whether called postulates or axioms, the important point is that my theory is deduced from Euclid’s five postulates plus one more of my own, the axioms describing equivalence relations, total orderings, additive groups, and from nothing else! I do not present – without proof – theorems that can only be proven with calculus in a vain attempt to convince students that I had proven them from the axioms of geometry. I do not casually assume the field axioms for real numbers nor do I employ the method of superposition. Robin Hartshorne (Geometry: Euclid and Beyond, p. 2) writes, “The method of superposition used [by Euclid] in the proof of [Book I, Proposition 4, SAS Congruence], which allows one to move the triangle so that it lies on top of the triangle , cannot be justified from the axioms.” I fully agree! I do not employ transformations, which are computer generated demonstrations of the method of superposition. And I do not use the Similarity/Dilation Axiom; I prove the triangle similarity theorem.

Common Core geometry textbooks state the triangle similarity theorem as an axiom, called either the similarity axiom or the dilation axiom, and then state without proof the AA, SAS and SSS similarity theorems. Triangle congruence theorems are then just special cases of the similarity/dilation axiom with the scale (dilation factor) being the multiplicative identity. The mid-segment theorem is a special case of the similarity/dilation axiom with the scale (dilation factor) being half. Along the way, the transversal theorems are also stated without proof.

That is the fastest path through geometry ever! But what did the students learn beyond memorizing formulas? They certainly did not learn anything about deductive logic. From their point of view, all of these statements are just factoids to be memorized. Learning about proofs is a charade. The fact that their teacher and the author of their textbook have put themselves above the need to prove their statements does not go unnoticed. Demanding that students “prove” their statements on exams by citing these unproven factoids smacks of demagoguery.

The biggest difference between this textbook and Common Core textbooks is that I do not put myself above the need to prove what I say and that I carry out these proofs with a small number of clearly stated assumptions. I do not silently assume the field axioms for real numbers; when the time comes (Volume Two), multiplication will be formally introduced. Nor do I make grand assumptions like the similarity/dilation axiom from whence every theorem is a special case.

I start with Euclid’s five postulates plus one more of my own; also, I cite the well-known axioms describing equivalence relations, total orderings and additive groups; I go until I have proven everything I know how to. Then I stop. That is all; nothing more, nothing less.

The way that you wander, is the way that you chose,
The day that you tarry, is the day that you lose,
Sunshine or thunder, a man will always wonder,
Where the fair wind blows, where the fair wind blows.

If you are coming to this table of contents now for the first time, it may seem as though a black belt in Geometry–Do is a mountain too high to climb. But I tell you, the next two years are going to pass anyway, so why not go for the gold? It is an accomplishment you can boast about for the rest of your life. What else can you do as a teenager that you will be proud of as an old man?

Comparison with Common Core Geometry

First-Day Exam in Geometry

White Belt Geometry for Construction Workers

The Egyptian or 3–4–5 Right Triangle

Basic Principles for Design of Wood and Steel Structures

Fortification Construction as an Application of Geometry

Segment	Two points fully define a segment.
Triangle	Three points fully define a triangle.
Line	A segment fully defines a line.
Circle	The center and the radius fully define a circle.
Right Angle	All right angles are equal to each other.
Parallel	A line and a point not on it fully define the parallel through that point.

Segments are denoted with a bar, \(\overline{EF}\); rays with an arrow, \(\overrightarrow{EF}\); lines with a double arrow, \(\overleftrightarrow{EF}\); and angles as \(\angle EFG\). The postulates are in terms of fully defined, which means that a figure with the given characteristics is unique, if it exists. Under defined means figures with the given characteristics are legion; more information is needed. John Playfair stated the parallel postulate roughly as I and David Hilbert do, which can be proven to be equivalent to Euclid’s Fifth Postulate.

If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

While Hilbert and I both found Euclid’s postulate to be convoluted and chose Playfair’s version, and we both reject real numbers as unsupported by our postulates, we otherwise took separate paths. Geometry–Do is like Hilbert’s geometry, but it is unique and has its own postulates.

Euclid also had five “common notions,” which vaguely describe what modern mathematicians call equivalence relations, total orderings and additive groups.

A relation is an operator, R , that returns either a “true” or a “false” when applied to an ordered pair of elements from a given set. For instance, if the set is integers and the relation is equality, then \(5=5\) is true, but \(5=4\) is false. Relations must be applied to objects from the same set. For instance, \(\overline{EF} = \angle G \) is neither true nor false; it is incoherent. There are four ways that relations may be characterized. It is never true that a relation has all four, but some have three.

Reflexive	a R a
Symmetric	a R b implies b R a
Anti-Symmetric	a R b and b R a implies a= b
Transitive	a R b and b R c implies a R c

A relation that is reflexive, symmetric and transitive is called an equivalence relation. The equivalence relations considered in geometry are equality ,=, which applies to segments, angles or areas; congruence ,\(\cong\), which applies to triangles; similarity,\(\sim\) , which applies to triangles; and parallelism, \(||\), which applies to lines. \(\overleftrightarrow{EF}||\overleftrightarrow{GH}\) means that \(\overleftrightarrow{EF}\) and \(\overleftrightarrow{GH}\) do not intersect.

Since segments are known only by their length, \(\overline{EF}=\overline{GH}\) means that \(\overline{EF}\) and \(\overline{GH}\) are the same length. It does not mean that they are the same segment; they may be in different locations. Since length is the same regardless of direction, it is always true that \(\overline{EF}= \overline{FE}\). But triangles are known, not by just one magnitude, but by six. The vertices are ordered to show which ones are equal. \(\overline{EFG}\cong\overline{HIJ}\) means that \(\overline{EF}=\overline{HI}\), \(\overline{FG}=\overline{IJ}\) ,\(\overline{GE}=\overline{JH}\) ,\(\angle E\cong\angle H\) ,\(\angle F\cong\angle I\) and \(\angle G\cong\angle J\). Beware! Writing the vertices of a triangle out of order is one of the most common mistakes made by beginning geometers, and it is always fatal to a proof.

A quadrilateral is a union of two triangles; congruence or similarity holds if and only if both pairs of triangles are congruent or similar. If \(\overline{EFG}\cong \overline{IJK}\) and \(\overline{EHG}\cong \overline{ILK}\), then, \(\overline{EFHG}\cong \overline{IJLK}\). Analogously, if \(\overline{EFG}\sim \overline{IJK}\) and \(\overline{EHG}\sim \overline{IKL}\), then, \(\overline{EFGH}\sim \overline{IJKL}\). Similarity is defined as two triangles with all corresponding angles equal, so \(\overline{EFG}\sim \overline{IJK}\) and \(\overline{EHG}\sim \overline{ILK}\) means that six pairs of corresponding angles are equal. This is more than just saying that the four corresponding interior angles of \(\overline{EFGH}\) and \(\overline{IJKL}\) are equal; thus, it is not true that proving these four equal is sufficient to prove \(\overline{EFGH}\sim \overline{IJKL}\). A counter-example is a square and a rectangle; they both have all right angles, but they are not similar. This is one reason why we do not define quadrilaterals as four-sided figures. This is a vacuous definition that has led many beginners to err by claiming that a square and a rectangle are similar. Also, our definition makes quadrilaterals a continuation of triangles; American schools have these as semester programs that can be taken in either order.

A relation that is reflexive, symmetric and transitive is an equivalence relation and there are four in geometry: equality, congruence, similarity and parallelism. Relations that are anti-symmetric can only be defined if we have already defined equality, because equality is referenced in its definition. A relation that is transitive, reflexive and anti-symmetric is called an ordering. Geometers only consider one: less than or equal to,\(\leq\) . An ordering is total if \( a \leq b \) or \( b \leq a \), always. A set with both an equivalence relation,= , and a total ordering, \(\leq\), is called a magnitude. There exist orderings that are not total, such as subset, but these are not used in geometry. Less than, \(<\) , means \(\leq\) but not =. It cannot be defined until both \(\leq\) and \(=\) have been defined.

Note that our definition of magnitude does not imply that real numbers can be associated with lengths, angles or areas; only that the relations \(=\) and \(\leq\) exist and have the required properties. It does imply that magnitudes are unique, which is what the replication axiom below is stating.

Equal magnitudes are an equivalence relation and can be reproduced wherever needed; that is, compasses do not collapse when lifted from the paper but are like holding a rope at a length. Compasses that collapse would be like surveyors who can walk a rope around an arc but, the moment the center guy takes a step, their rope turns to smoke. Because errors accumulate, it is not possible to put hash marks every foot – a quarter-inch error in every mark is an error of several feet per hundred yards – plus shrinkage or expansion as temperature and humidity change. This is why we use a straight edge, not a ruler; but the idea that a compass cannot be lifted off the paper to mark a length elsewhere makes geometry a parlor game, not a science.

An equivalence class is a set of objects that are equal, congruent, similar or parallel to each other. Equivalence classes can be defined in reference to an existing equivalence class. For instance, if an equivalence class is defined as all the angles equal to a given angle, then all the angles complementary to any member of that class are equal to each other; that is, they form their own equivalence class. All the angles supplementary to any member of that class are also equal to each other. If an equivalence class is defined as all the lines parallel to a given line, then all the lines perpendicular to any member of that class are parallel to each other. All the circles with radii equal to any member of an equivalence class of equal segments are an equivalence class.

Equivalence also refers to statements that can be proven if the other one is assumed, and in either order. For instance, Euclid’s fifth postulate and Playfair’s postulate are equivalent because, assuming either to be true, it is possible to prove that the other is true. The equivalence of theorems can be expressed by separating them with the phrase “if and only if,” which can be abbreviated “iff.” Proof in the other direction is called the converse; that is, if \(X\) implies \(Y\), then the converse is that \(Y\) implies \(X\). If \(X\) and \(Y\) are equivalent, then both implications are true.

Proof by contradiction when there is only one alternative that must be proven impossible is called a dichotomy. A trichotomy (e.g. ASA congruence) has three alternatives. A magnitude can either be less than, equal to or greater than another, and only one of these three is desired; thus, by proving the other two to be impossible, we know that it is the one that makes the theorem true.

We define an additive group as a set and an operation (addition) that has these properties:

Associative property	\((a+b)+c=a+(b+c)\)
Commutative property	\(a+b=b+a\)
Existence and uniqueness of an identity	\(a+0=a=0+a\)
Existence of inverses (identity is its own)	\(a+(-a)= 0 =(-a)+a\)

There exist magnitudes that are not additive groups, such as economic value. Given a choice between \(a\) or \(b\), it is always possible for a person to choose one above the other. But, because \(a\) may substitute for or be a complement to \(b\), they are not independent the way geometric magnitudes are. There are also additive groups that cannot be ordered, such as matrices. Matrices of the same dimension are an additive group, but we cannot say \(a \leq b\) for any two.

On the first day of class I ask the students to look back to a time eight or ten years prior, when they were little kids and knew only how to add and subtract; multiplication and division was still scary for them. I assure them that geometry will be like going back to 1st grade. Sticking segments together end to end or angles together side by side is no more difficult than 1st grade problems about adding chocolates to or subtracting chocolates from a bowl of candies. How easy is that?

Replication Axiom
Given \(\overline{EF}\) and \(\overrightarrow{E'G'}\), there exists a unique point F' on \(\overrightarrow{E'G'}\) such that \(\overline{EF}\)=\(\overline{E'F'}\). Given \(\angle EFG\) and \(\overrightarrow{F'E'}\), on a side of \(\overrightarrow{F'E'}\) there exists a unique ray \(\overrightarrow{F'G'}\) such that \(\angle EFG\)=\(\angle E'F'G'\).

Interior Segment Axiom
If \(G\) is between \(E\) and \(F\) then \(\overline{EG}<\overline{EF}\), then \(\overline{GF}<\overline{EF}\) and \(\overline{EG}+ \overline{GF}=\overline{EF}\)

Interior Angle Axiom
If \(H\) is inside \(\angle EFG\), then \(\angle EFH < \angle EFG\) and \(\angle HFG< \angle EFG\) and \(\angle EFH+ \angle HFG= \angle EFG\).

Pasch’s Axiom
If a line passes between two vertices of a triangle and does not go through the other vertex, then it passes between it and one of the passed vertices.

To be between \(E\) and \(F\) means to be on the segment they define, \(\overline{EF}\), but at neither endpoint. To be inside \(\angle EFG\) means to be between points on \(\overrightarrow{FE}\) and on \(\overrightarrow{FG}\) , with neither point being \(F\). It is instinctive that all humans know what it means for a point to be between two points and – in the case of Pasch’s axiom – also what it means for a segment to be continuous; that is, with no gaps where another segment might slip through. Triangles and quadrilaterals are defined to be convex; the segment between two points interior to two sides is inside the figure. This means that they are not allowed to be concave or degenerate. Interior angles are greater than zero and less than straight, so triangles are never segments and quadrilaterals are never triangles or darts.

In Geometry–Do, between, inside, plane, point, shortest path and straight are undefined terms. These are concepts that a parent does not have to explain to a child; they are just giving names to concepts that are already in the child’s mind. Area is defined as the number of squares that fill a triangle or union of triangles. Like the ancient Greeks, we do not have a rigorous definition of limits but just rely on intuition; wheat plants are infinitesimal compared to fields, so weighing the wheat is almost like calculating a limit. Thus, area too is something that small children can understand without explanation. Defining area as the product of a rectangle’s sides waits for Volume Three: Geometry with Multiplication. This definition of area is not intuitive to small children, who know nothing of multiplication, which is why it is introduced late in our study.

Degrees of angle will not be defined anywhere in Geometry–Do because doing so is trigonometry.

Triangle Inequality Theorem
Any side of a triangle is shorter than the sum of the other two sides.

In ancient Greece, Epicurus scoffed at Euclid for proving a theorem that is evident even to an ass (donkey), who knows what the shortest path to a bale of hay is. Indeed, it is a direct result of our definition that a segment is all the points along the shortest path between two points. It is an exercise for yellow belts to prove it using the greater angle and greater side theorems, but we will satisfy both Epicurus and Euclid by introducing it among the axioms while calling it a theorem.

The foundations explained above are sufficient through blue-belt study. In these early chapters, students will learn to bisect, trisect and quadrisect a segment, and to multiply it by small natural numbers by using repeated addition. No more of these repeated additions are needed than four, for construction of the Egyptian or 3–4–5 right triangle, the only exception being that we mention in passing the 5–12–13 right triangle, which is used by plumbers when installing 22.5° elbows.

Beginners, especially construction workers anxious to complete white-belt geometry, are advised not to get too hung up on these foundations, which are a bit abstract. But it is essential that we lay a solid foundation for our science. It is recommended that students read again about foundations when they are orange belts and are more comfortable with abstract reasoning. (Also, SSS and ASS, mentioned in the first paragraph, will then be known to them.) By then, those who are not – the construction workers – will be gone. Red belts are expected to teach beginning students to relieve black belts of this task. Pedagogical instruction is provided to red belts for this purpose, and they are also asked to read this foundational material yet again, and deeply.

Black belts will learn of similarity and prove the triangle similarity theorem, which Common Core students take as a postulate because they do not really know how to prove anything. Similarity opens up a whole new world in geometry! Specifically, black belts will go beyond bisecting and trisecting segments to constructing segments whose length relative to a given unit is any rational number. But, for this, another axiom is needed. We have said that a set with both an equivalence relation, \(=\) , and a total ordering, \(\leq\) , is called a magnitude. But to construct segments whose length relative to a given unit is any rational number, length must also be Archimedean.

Archimedes’ Axiom
Given any two segments \(\overline{EF}\) and \(\overline{GH}\), there exists a natural number,\(n\) , such that \(n\overline{EF}>\overline{GH}\).

This may seem trivially true, but Galois (finite) fields are not Archimedean. Every school boy is taught that Archimedes claimed that, given a long enough lever and a fulcrum to rest it on, he could move the world. They typically receive no clear answer from their teacher on why it matters, since no such fulcrum exists and Archimedes seems to ignore that gravity is attractive. The point that Archimedes is making is that, if there were such a fulcrum and much gravity under it, he would need a lever \(6\times10^{22}\) longer on his side of the fulcrum to balance his mass against the Earth. If the fulcrum were one meter from Earth, Archimedes would be in the Andromeda galaxy if he stood on the other end of that long lever. \(6\times10^{22}\) is a big number, but it does exist.

We said above that undefined terms are concepts that one does not have to explain to a child; the adult is just giving names to concepts that are already in the child’s mind. But defining natural numbers as \(1,2,3..\) is only intuitive up to as many fingers as the child has. When I took my four-year-old to another town, she was surprised that a different man was driving the bus. She thought that the few dozen people she had met in our town represented everybody in the world; that is, she thought that the natural numbers are a Galois field modulo \(47\). We think \(6\times10^{22}\) exists because countably infinite fields are consistent; but so are big Galois fields. This axiom is why it is traditional in America to tell children that every snowflake is unique⁹. That Archimedes’ axiom is not intuitive to small children is one reason why similarity is delayed until black belt.

But these are issues of concern to black belts; first, the student must take a short jog through the colored belts, which are concerned with what Mihalescu refers to as the remarkable elements of triangles and quadrilaterals. By this we initially mean the principal triangle centers. The medians intersect at the medial point, the angle bisectors intersect at the incenter, the altitudes intersect at the orthocenter, and the mediators intersect at the circumcenter. Here, in the introduction, the student does not need to know what any of these things are, only that medians – the segment from a vertex to the midpoint of the opposite side – and the bisectors of vertex angles are always inside their vertex angle. In \(\overline{EFG}\), if the vertex is F, then they are inside \(\angle EFG\).

Crossbar Theorem
Given triangle \(\overline{EFG}\) and a point P inside it, the ray \(\overrightarrow{EP}\) intersects the line segment \(\overline{FG}\).

Proof
Let Q be on the ray \(\overrightarrow{GE}\) so E is between G and Q. Consider the triangle \(\overline{QFG}\). The line \(\overleftrightarrow{EP}\) passes between the vertices Q and G because E is between G and Q, and it does not pass through the other vertex, F, because P is inside \(\overline{EFG}\), which means that it is not on \(\overline{EF}\). Thus, the conditions of Pasch’s Axiom are met and \(\overleftrightarrow{EP}\) must intersect either \(\overline{FG}\) or \(\overline{EF}\). Suppose \(\overrightarrow{EP}\) intersects \(\overline{EF}\) at J. Since a segment fully defines a ray, \(\overrightarrow{EJ}\) and \(\overrightarrow{EF}\) are the same ray, which is a contradiction because P is on \(\overrightarrow{EJ}\) but not on \(\overrightarrow{EF}\). Thus, \(\overrightarrow{EP}\) does not intersect \(\overline{EF}\). The ray in the other direction of \(\overrightarrow{EP}\) does not intersect either \(\overline{FG}\) or \(\overline{EF}\)EF because both segments are on the other side of \(\overline{GQ}\). Thus, \(\overrightarrow{EP}\) intersects \(\overline{FG}\).

The midpoints of segments are denoted by the letter M with a double subscript, which are the endpoints of the segment. Thus, two medians of the triangle \(\overline{EFG}\) are \(\overline{EM_{FG}}\) and \(\overline{FM_{GE}}\). Consider the triangle \(\overline{EM_{FG}G}\). The line \(\overleftrightarrow{FM_{GE}}\) passes between the vertices G and E because \(M_{GE}\) is between G and E, and it does not pass through the other vertex, \(M_{FG}\), because \(M_{FG}\) is not F. Thus, the conditions of Pasch’s Axiom are met and \(\overleftrightarrow{FM_{GE}}\) must intersect either \(EM_{FG}\) or \(M_{FG}G\). Since it intersects \(\overleftrightarrow{M_{FG}G}\) at F, it cannot also intersect this line in the segment \(M_{FG}G\). Thus, it intersects \(EM_{FG}\). This proves that the medial point of a triangle is always inside the triangle.

Analogously, the incenter of a triangle is always inside the triangle. The only difference in the proof is that, instead of knowing that the bisectors of vertex angles E and F intersect the opposite sides at \(M_{FG}\) and \(M_{GE}\), respectively, we must first invoke the crossbar theorem to prove that they intersect the opposite sides somewhere on them, and give these points labels; say, E* and F*

By the triangle postulate, three points fully define a triangle and, since the medial point and the incenter have now been proven to be inside the triangle, they are fully defined. Because we nowhere invoked the parallel postulate in the preceding proofs, medial points and incenters always exist in absolute geometry and are thus topics of discussion for white and yellow belts.

But what about the orthocenter? Altitudes are only inside acute vertex angles so, without the parallel postulate, white and yellow belts may only discuss the orthocenter if the triangle is known to be acute. By a somewhat more involved argument, the circumcenter also exists for acute triangles. Sometimes these centers exist for triangles that are not too obtuse, though giving a precise meaning to “not too obtuse” is beyond the scope of this book; thus, white and yellow belts are advised to just defer most discussions of these triangle centers to orange belt.

\(\alpha, \beta, \gamma, \delta\)	Angles of a triangle or quadrilateral; usually \(\angle E, \angle F, \angle G, \angle H, respectively.
\(\rho, \sigma, \varphi\)	\( \rho\) is right and \(\sigma\) is straight. \(\varphi\) is the interior angle in an equilateral triangle.
\(E, F, G, .., W\)	Points. Do not use H, I,M, O, R arbitrarily; they have assigned meanings.
\(M, I, X, Y, Z\)	\(M\) is usually a midpoint; subscripts denote of what; e.g. MEF is of \(\overline{EF}\). I is the incenter and X, Y, Z the excenters of a triangle; subscripts denote touching points. Otherwise, double subscripts denote the reflection of a point around a line; \(T_{EF}\) is the reflection of T around the line \(\overleftrightarrow{EF}\).
E', F', G'	The feet of altitudes from E, F, G in \(\overline{EFG}\); or the feet of perpendiculars
E*, F*, G*	The intersection of angle bisectors with the opposite side of a triangle
u, v, w	The legs and hypotenuse of a right triangle, respectively
a, b, c	The coefficients of \(ax^{2}+bx+c=0\); not the sides of a right triangle.
H, h	H is usually a triangle’s orthocenter, unless it is the fourth vertex of a quadrilateral. h is the height of a triangle, or of a parallelogram.
A, B, C, D, d	A is the area of a triangle or quadrilateral; e.g. \(\overline{EFG}\) has area A=\(|\overline{EFG}|\); B is the length of the base of a triangle or quadrilateral; C is a triangle’s medial point or a parallelogram’s bi-medial point; D is the circumdiameter; and d is the indiameter. Do not use these letters arbitrarily!
P	A point, usually significant. \(P_{E}, P_{F}, P_{G}\) are the pedal vertices of P in \(\overline{EFG}\)
\(L_{E}, L_{F}, L_{G}\)	Long centers of \(\overline{EFG}\), where the mediators and angle bisectors meet on \(\omega\)
r, R	The radii of the incircle and of the circumcircle, respectively
s	The semiperimeter of a triangle or quadrilateral
\(\omega, O\)	ω (omega) is a circle, usually the circumcircle. O is usually a circle’s center.
\(\equiv, \cap, \cup, -\)	Coincident (the same thing), intersection, union and removal from a union
\(\perp, \parallel, \not\parallel, \cong, \not\cong \)	Perpendicular, parallel, not parallel, congruent, not congruent and similar

Side–Angle–Side (SAS) Theorem
Given two sides and the angle between them, a triangle is fully defined.

Proof Illustration
By the segment postulate, the segments have two endpoints and, since they form an angle, they share an endpoint. This is three so, by the triangle postulate, the triangle is fully defined. Congruence is transitive, so any two anywhere are congruent.

Euclid had five postulates, not six, but proof of his fourth proposition, SAS congruence, relied on superposition, which tacitly assumes a whole slew of additional and unmentioned postulates. Many have cast doubt on Euclid, pointing out that superposition – sliding figures around and flipping them over to position one on top of the other – is nowhere defined.

Robin Hartshorne (Geometry: Euclid and Beyond, p. 2), writes, “Upon closer reading, we find that Euclid does not adhere to the strict axiomatic method as closely as one might hope… The method of superposition… cannot be justified from the axioms… we can develop geometry according to modern standards of rigor.” But, when Common Core was formulated, Hartshorne was shunted aside because Bill Gates was offering big money to redefine congruence in terms of transpositions – sliding figures around on a computer screen to superimpose them – assuring that geometry ceases to exist the moment a student rises from his school computer. By this definition, is a 3–4–5 triangle drawn in this book congruent to one drawn on the wall of a 4000-year-old pyramid in Egypt? Neither moved! For that matter, did a figure in this book fly through the air and land on your homework?

Isosceles Triangle Theorem
If two sides of a triangle are equal, then their opposite angles are equal.

Proof Illustration
Given \(\overline{EFG}\) with \(\overline{GE}\) and \(\overline{GF}\) equal, by the line postulate, draw \(\overrightarrow{GE}\) and \(\overrightarrow{GF}\) and cut them off at \(H\) and \(I\) so \(\overline{EH}=\overline{FI}\) and \(\overline{GH}=\overline{GI}\) by addition. By SAS,\(\overline{FGH}\cong\overline{EGI}\). By congruence, \(\angle GHF=\angle GIE\) and \(\overline{HF}=\overline{IE}\). By SAS,\(\overline{EHF}\cong\overline{FIE}\) and \(\angle FEH=\angle EFI\). By subtraction, if the exterior angles are equal, then so are the interior angles,\(\angle FEG=\angle EFG\). .

Observe that, when we cite SAS, the triangle vertices are ordered by the side, angle and side that are equal; e.g. \(\overline{FGJ}\cong\overline{EGK}\) by SAS means that \(\overline{FG}=\overline{EG}\) and \(\angle FGJ=\angle EGK\) and \(\overline{GJ}=\overline{GK}\) are given and other equalities, such as \(\angle GJF=\angle GKE\) and \(\overline{JF}=\overline{KE}\), are implied. Also, \(\overline{FGJ}\cong\overline{EGK}\) implies equal areas; \(|\overline{FGJ}|=|\overline{EGK}|\). The contrapositive is \(|\overline{FGJ}|\neq|\overline{EGK}|\) implies \(\overline{FGJ}\cong\overline{EGK}\).

Equilateral Triangle Theorem Illustration
If three sides of a triangle are equal, then all three angles are equal.

Proof of the SSS theorem will use a proof by contradiction; that is, show that Y not true and X true is contradictory. We have defined dichotomy and trichotomy; now we assume that G and H are distinct and then consider the four places where H can be if it is not G. Like aiming a rifle at a target, there are only five possibilities: a bull’s eye or a miss to the left, right, above or below. We show that the latter four are impossible. The lemma is based on what “inside” means.

Lemma 1.1 Illustration
If a triangle is inside another triangle, it has less area.

Side–Side–Side (SSS) Theorem
Given the three sides, a triangle is fully defined.

Proof Illustration
Given \(\overline{EFG}\) and \(\overline{EFH}\) with \(\overline{EG}=\overline{EH}\) and \(\overline{FG}=\overline{FH}\), suppose that \(G\) and \(H\) are distinct. By lemma 1.1, if \(H\) is inside \(\overline{EFG}\) or inside the angle vertical to \(\angle EGF\), then \(|\overline{EFH}|<|\overline{EFG}|\) or \(|\overline{EFH}|>|\overline{EFG}|\), which implies \(\overline{EFG}\neq\overline{EFH}\). Suppose \(H\) is on the \(E\) side of \(\overline{FG}\) but not inside \(\overline{EFG}\).\(\overline{EG}=\overline{EH}\), so \(\overline{EGH}\) is isosceles. \(\angle EHG=\angle EGH\) by the isosceles triangle theorem. By analogous reasoning, \(\overline{FGH}\) is isosceles and thus \(\angle FGH=\angle FHG\).

\(\angle EHG=\angle FHG+\angle EHF\)	and by analogous reasoning	\(\angle FGH=\angle EGH+\angle FGE\)
\(\angle EHG>\angle FHG\)		\(\angle FGH>\angle EGH\)
\(\angle EHG>\angle FHG\)		\(\angle FGH>\angle EHG\)

A contradiction; \(H\) on the \(F\) side of \(\overrightarrow{EF}\) but not inside \(\overline{EFG}\) is also contradictory.

Fully defined does not imply existence – the longest segment must be less than the sum of the other two – but it does imply uniqueness so, by transitivity, any two anywhere are congruent.

In the following construction, existence and uniqueness of \(\overrightarrow{FE}\) and \(\overrightarrow{FG}\) requires invoking the line postulate, though this goes unsaid. In the same way that, given \(E\) and \(F\), we speak of \(\overline{EF}\) without bothering to invoke the segment postulate, we now speak of \(\overrightarrow{FE}\) or \(\overleftrightarrow{FE}\) whenever \(\overline{FE}\) has been defined. This practice is in keeping with our plan to avoid tedious proofs with mincing steps, but the student should never forget that Euclid’s postulates are ever-present and needed.

Construction 1.1
Bisect an angle.

Solution Illustration
Given \(\angle EFG\), take any point H on \(\overrightarrow{FE}\). There exists a point I on \(\overrightarrow{FG}\) such that \(\overline{FH}=\overline{FI}\). Construct an isosceles triangle with base \(\overline{JK}\) and \(L\) apex on the other side of \(\overline{JK}\) from \(F\). By SSS, \(\overline{JFL}\cong\overline{KFL}\), which holds the equality \(\angle JFL=\angle KFL\)

To construct an isosceles triangle when the base is given, a geometer sets his compass to any length longer than half the base and draws arcs from each endpoint. Where these arcs intersect is an apex; there are two possible, one on each side of the base. These arcs are each called a locus, and together, loci. To construct an isosceles triangle when the apex angle is given, lay off the same arbitrary length on both of the rays from the vertex and then connect these points.

Construction 1.2
Bisect a segment.

Solution Illustration
Given \(\overline{EF}\), construct an isosceles triangle with \(\overline{EF}\) as base. Using C. 1.1, bisect the apex angle. Since the sides are equal, there is no need to find H and I; just use E and F. By SAS, the angle bisector intersects \(\overline{EF}\) at its midpoint.

Construction 1.3
Raise a perpendicular from a point on a line.

Solution Illustration
Given \(\overleftrightarrow{EF}\) with G on it, lay off the same arbitrary length to the left and to the right of G and then construct an isosceles triangle with this base. By SSS, the segment connecting the apex with G forms congruent triangles and the angles at G are right.

Construction 1.4
Drop a perpendicular from a point to a line.

Solution Illustration
Given G not on \(\overleftrightarrow{EF}\), construct an isosceles triangle with apex G and base collinear with \(\overleftrightarrow{EF}\). Using C. 1.1, bisect the apex angle. By SAS it forms congruent triangles and the angles at its intersection with \(\overleftrightarrow{EF}\) are right.

These constructions are the four basic techniques that will be used in combination throughout geometry. At the most fundamental level, all four are much alike. This is analogous to how the jab, hook, uppercut and cross are the basic techniques that are used in combination throughout boxing. But all four involve giving somebody a poke in the nose, so they are much alike.Did you get the equilateral triangle theorem? You only had two theorems in your kit! Like a carpenter who only owns a claw hammer, for every nail, he’s either going to hit it or pry it out. What else?

The perpendicular bisector of a segment is called its mediator. The perpendicular from a triangle vertex to the (extension of the) opposite side is called an altitude. Red belts will extend altitudes past the opposite side and will extend the bisector of an interior angle past the opposite side, but when lengths are assigned to an altitude or to an angle bisector, it means the length of the segment from the vertex to the opposite side.

Center Line Theorem
An angle bisector and a perpendicular bisector coincide if and only if the triangle is isosceles.

Proof Illustration
Assume the angle bisector and perpendicular bisector coincide. By SAS (reflexivity, the right angle postulate and bisection), the two right triangles are congruent and so their hypotenuses are equal. Thus, the given triangle is isosceles.

Assume the triangle is isosceles. By the isosceles triangle theorem, the base angles are equal. Construct a median from the apex. By SAS(opposite sides, opposite angles and bisection), the two triangles are congruent. The apex angle is bisected and the angles at the foot of the median are equal; right, because they bisect a straight angle.

The center line is the mediator of the base and the apex angle bisector of an isosceles triangle.

Construction 1.5
Replicate an angle.

Solution Illustration
Construct an isosceles triangle with the given angle as its apex angle by laying off equal lengths and connecting them. By SSS, reconstruct this triangle elsewhere.

Construction 1.6
Given a ray and a point on the angle bisector, find the other ray of the angle.

Solution Illustration
Around the endpoint of the ray, draw an arc through the point. Then draw a circle around the point through the intersection of the arc and the ray. Then draw a ray from the endpoint of the given ray through the other intersection of the arc and the circle.

Interior and Exterior Angles Theorem
The bisectors of an interior and exterior angle of a triangle are perpendicular to each other.

Proof Illustration
Given \(\overline{EFG}\) and \(J\) on \(\overrightarrow{EF}\) past \(F\),\( \angle EFG\) is the interior angle and \(\angle JFG\) is the exterior angle at vertex \(F\). By C. 1.1, find \(K\) and \(L\) on the angle bisectors of \(\angle EFG\) and \(\angle JFG\), respectively. \(\angle EFK=\angle GFK\) and \(\angle JFL= \angle GFL\), so \(\angle EFK+\angle JFL=\angle GFK+\angle GFL\) by addition. The union of these four angles is a straight angle and, if a straight angle is cut in two equal angles, then each one is right; thus, \(\angle GFK+\angle GFL=\rho\) and \(\overrightarrow{FK}⊥\overrightarrow{FL}\).

Reflection Theorem Illustration
If \(\overline{EFG}\) is isosceles with base \(\overline{EF}\), then \(\overline{EFG}\cong\overline{FEG} \) and \(\overline{EFG}\sim\overline{FEG} \)

The important lesson to be taken from this theorem is that the order of the vertices matters. \(\overline{EFG}\) and \(\overline{FEG}\) are different triangles, so \(\overline{EFG}\cong\overline{FEG}\) is a meaningful statement; it is not proven by transitivity. By the isosceles triangle theorem, \(\overline{FG}=\overline{EG}\). \(\overline{EFG}\cong\overline{FEG}\) by SSS is shorthand for \(\overline{EG}=\overline{FE}\) and \(\overline{FG}=\overline{EG}\) and \(\overline{GE}=\overline{GF}\). It saves a lot of time if order of the vertices contains meaning, but the system only works if people are conscientious about ordering them correctly.

Problem 1.1
Draw a line through a point so it makes equal angles with the sides of an angle.

Solution Illustration
By the Isosceles Triangle Theorem Converse, the desired line is the base of an isosceles triangle with the given angle at its apex. By the Center Line Theorem, the base is perpendicular to the apex angle bisector.

Just solving a problem is not enough; you must also explain in what situations your solution might fail. One can always drop a perpendicular on a line, but not always on a ray, so this may not work.

Problem 1.2 Illustration
A fink truss consists of an equilateral triangle built on the middle third of the ceiling joists. The rafters rest on the walls and meet at the triangle apex. Beams from the feet of the triangle meet the rafters at right angles. Draw it. The boards need not have width.

The fink truss leaves the middle open for storage or for a mattress, making it the best choice for a shed or a mountain cabin. For flatter roofs, drop a vertical from the apex and from each rafter midpoint and angled beams from the center to the rafter midpoints. The strongest is the king post truss, a vertical from a right apex and angled beams from its foot to the rafter midpoints.

Problem 1.3
Suppose your girlfriend asks you to install a wall mirror. She is six feet tall in heels and her eyes are six inches below the top of her hair. What is the smallest mirror that allows her to see her entire self and how high should it be above the floor? Does it matter how far away she stands?

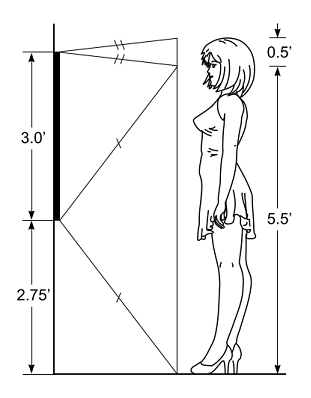
Construct two isosceles triangles with bases from her eyes to her feet and to the top of her hair.

The mediator theorem, in the exit exam, is bi-conditional and so it requires two independent proofs, as did the center line theorem. The student must assume that a point is on the perpendicular bisector and prove that it is equidistant from the endpoints of the segment; and, in a separate proof, he must assume that a point is equidistant from the endpoints of a segment and prove that it is on the perpendicular bisector. The two proofs may be done in either order.

Technically, p and q are equivalent even if proof that q implies p requires citing the previously proven statement that p implies q. However, students see it as a trick if I say, “prove that p and q are equivalent,” but I do not mention that they must prove that p implies q first, and then prove that q implies p. No tricks! If this is the case, then I will call the statement that p implies q a theorem, and the statement that q implies p its converse, but I will not call them equivalent.

Mediator Theorem
A point is on the perpendicular bisector iff it is equidistant from the endpoints of the segment.

Saccheri Theorem I
If \(\overline{EFGH}\) is a Saccheri quadrilateral, so \(\angle E=\angle F=ρ \)and \(\overline{EH}=\overline{FG}\), then \(\angle H=\angle G\).
(1)\(\overline{EG}=\overline{FH}\); (2) \(\angle G=\angle H\); (3)\(\overleftrightarrow{M_{EF}M_{GH}}\bot\overleftrightarrow{EF} \) and \(\overleftrightarrow{M_{EF}M_{GH}}\bot\overleftrightarrow{GH} \).

Construct each triangle using only the information given about it.

1.4 Construct a right triangle given the lengths of the legs.

1.5 Construct a triangle given the lengths of the three sides.

1.6 Construct a triangle given the apex angle and the lengths of the legs.

1.7 Construct a triangle given the lengths of the base, the median to the base and one leg.

1.8 Draw a king post roof truss with a right apex. The boards need not have width.

1.9 Ancient hieroglyphics describe a 350’ tall pyramid that no longer exists. Could a Common Core student prove it congruent to the Luxor hotel in Las Vegas by using transposition?

1.10 Construct an equilateral triangle, \(\overline{EFG}\). In the Notation section, we define \(\varphi\) to be the interior angle of an equilateral triangle. Is this the same thing as defining it to be a third of a straight angle? Is \(\overline{M_{EF}M_{FG}M_{GE}}\) equilateral in hyperbolic geometry, or only Euclidean? Can you prove that the interior angles of \(\overline{M_{EF}M_{FG}M_{GE}}\) equal the interior angles of \(\overline{EFG}\)?

1.11 Most engineers use the metric system. Americans have a hybrid system that uses inches but, instead of those annoying 16th and 32nd parts, they divide them into 10th and 100th parts. Draw a segment 5.8'', raise perpendiculars at each endpoint and bisect the right angles to form an isosceles triangle with the angle bisectors meeting at the apex. How long are the legs in 10th of an inch? Would this also be true in hyperbolic geometry?

1.12 Given \(\overline{EFGH}\), if \(\overline{EG}=\overline{FH}\) and they bisect each other, prove that \(\overline{EF}=\overline{GH}\) and \(\overline{FG}=\overline{GH}\).

1.13 Given \(\overline{EFGH}\), if \(\overline{EF}=\overline{GH}\) and \(\overline{FG}=\overline{HE}\), prove that \(\overline{EFG}\cong\overline{GHE}\) and \(\overline{FGH}\cong\overline{HEF}\).

1.14 A carpenter constructs an A-frame with E and F the feet, G the apex, \(\overline{EG}=\overline{FG}\) and a crosspiece between \(M_{GE}\) and \(M_{FG}\), just like a commercial steel A-frame. But, when it is overloaded, the legs bow outward and start to pull free of the crosspiece. Reasoning that wood can take a compressive load but cannot pull things together while steel is just the opposite, he determines to connect \(\overline{EM_{FG}}\) and \(\overline{FM_{GE}}\) with wire rope. There are two different ways to prove that \(\overline{EM_{FG}}=\overline{FM_{GE}}\); write two independent proofs of this.

1.15 Diameters are the greatest chords. (They try not to let it go to their heads.) Diameter and chord are yellow-belt terms; look them up and then prove this to be true.

Common Core teachers present the isosceles triangle theorem after showing students the button on Geometer’s Sketchpad for bisecting a segment. They never demonstrate bisecting a segment with compass and straight edge; they rely heavily on that magical midpoint button.

Isosceles Triangle Theorem
If two sides of a triangle are equal, then their opposite angles are equal.

Common Core Proof
Given \(\overline{EFG}\) with \(\overline{GE}\) and \(\overline{GF}\) equal, use C. 1.2 to bisect \(\overline{EF}\) at \(\overline{M_{EF}}\). \(\overline{M_{EF}EG}=\overline{M_{EF}FG}\) By SSS, and thus \(\angle M_{EF}EG=\angle M_{EF}FG\)

Alternate Proof
Given \(\overline{EFG}\) with \(\overline{GE}\) and \(\overline{GF}\) equal, by SSS, \(\overline{EFG}\cong\overline{FEG}\) and thus \(\angle EFG=\angle FEG\)

The alternate proof is easier but, for reasons known only to David Coleman, was not chosen for Common Core. Both require SSS and thus neither can be used in Geometry–Do because the proof of SSS requires the isosceles triangle theorem. Coleman dodges the charge of circular reasoning by the simple expedient of not proving SSS. It, SAS and AAS (needed for the converse) are all just factoids for the students to memorize. Cheater! Cheater! Booger eater!

Isosceles Triangle Theorem Converse
If two angles of a triangle are equal, then the opposite sides are equal.

Common Core Proof
We are given \(\overline{EFG}\) with \(\angle E\) and \(\angle F\) equal. Use C. 1.1 to bisect \(\angle FGE\) and extend it to H on \(\overline{EF}\). By AAS, \(\overline{HEG}\cong\overline{HFG}\) and thus \(\overline{EG}=\overline{FG}\).

Common Core states the triangle similarity theorem as an axiom – we prove it in the black belt chapter – calling it either the similarity axiom or the dilation axiom, and then state without proof the AA, SAS and SSS similarity theorems. SAS, SSS, ASA, AAS and HL are then just special cases of the similarity/dilation axiom with the scale (dilation factor) being the multiplicative identity – which requires assuming the field axioms for real numbers – and the mid-segment theorem is a special case with the scale (dilation factor) being one half. Common Core students who claim to know of easier proofs to the isosceles triangle theorem and its converse can only say this because they did not have to prove SAS, SSS, ASA, AAS and HL. Common Core is just boring memorization!

The orange-belt chapter concludes with a section on how to pass a standardized exam of the type that is designed for Common Core students. Most of the people now reading these lines will not survive orange belt, so I will here tell you how a Geometry–Do white belt can pass Common Core exams. First, recognize that it is really an algebra exam in disguise, so review Algebra I. But the big secret is to bring a center-finding metric ruler and a compass to the exam so you can construct the figures – the ones provided are purposefully wrong – and measure the unknown quantity.

Varsity Tutors Advanced Geometry Exam, problem #14, is solved below, first using geometry and then using the algebra that masquerades as geometry in Common Core. Which is easier?

Problem 1.16 Illustration
Given a triangle with base 14 units and legs 13 and 15 units, what is the height?

Geometry Solution
Use SSS to construct the triangle and then measure its height. It’s 12!

Algebra Solution
Let x and y be the projections of the 13 and 15 unit legs on the base, respectively. Then \(x+y=14\) and, by the Pythagorean theorem, \(132=x^{2}+h^{2}\) and \(152=y^{2}+h^{2}\). Solve both equations for \(h^{2}\), set them equal and substitute \(y=14-x\) into the latter equation.

\(169-X^{2}=225-(14-x)^{2}\)
              \(=225-196+28x-X^{2}\)
          \(0=-140+28x \)
              \(x=\frac{140}{28}=5\)
Substitute \(x=5\) into the first equation, \(132=x^{2}+h^{2}\), and then solve it for h. \(h=\sqrt{169-25}=\sqrt{144}=12\)

Varsity Tutors considers this advanced because almost no American geometry student can answer it correctly or, if they do, it takes them thirty minutes to work through all the algebra. But, if you construct the geometric figure with a ruler and compass (Duh! It’s a geometry exam!), you can solve it in one minute using the most basic white-belt theorem you know.

Teachers! If you have read this far hoping for advice on how to get your #%$^@ students through the Common Core standardized exam, here it is: Ask for the perimeter of a triangle with vertices \((-2,3), (-4,-4), (-7,-1)\) and make it a race. The easy way is to lay the three sides end-to-end on a line. Taking the sum of three applications of the algebraic distance formula is the hard way.

\(\sqrt{(-2-(-7)^{2})+(3-(-1)^{2})}+\sqrt{(-2-(-4)^{2})+(3-(-4)^{2})}+\sqrt{(-7-(-4)^{2})+(-1-(-4)^{2})}\approx17.9\)

The first task of the high-school geometry teacher is to disabuse students of the notion that geometry is just a boring review of Algebra I. (Nothing new here. Blah!!!) You own a triangular pasture with vertices \((-2, 3), (-4,-4), (-7,-1)\), as measured in kilometers. To the nearest 100 meters, how long is the fence around it? Make it a race with the first solver getting an A.

The easy way is to lay the three sides end-to-end on a line. Put the compass pin at \((-7,-1)\) and rotate it to lay off the lower left side on the horizontal. Without moving the pin, measure the upper left side and lay it off on the horizontal past the one you just did. Finally, measure the upper right side and lay it off on the horizontal past the one you just did. It’s segment addition!

\(\sqrt{(-2-(-7)^{2})+(3-(-1)^{2})}+\sqrt{(-2-(-4)^{2})+(3-(-4)^{2})}+\sqrt{(-7-(-4)^{2})+(-1-(-4)^{2})}\approx18\)
\(\sqrt{(5)^{2}+(4)^{2}}+\sqrt{(2)^{2}+(7)^{2}}+\sqrt{(-3)^{2}+(3)^{2}}\)
\(\sqrt{25+16}+ \sqrt{4+49} + \sqrt{9+9}\)
\(\sqrt{41}+\sqrt{53}+ \sqrt{18}\)
\(\approx 6.40 + 7.28 + 4.24\)
\(\approx 17.92\)

Here is a PDF of this test: http://www.axiomaticeconomics.com/day_one_exam.pdf

If you have Common Core students who think they know something about geometry, ask for the medial point of a triangle with vertices \((-6.75,-6.75), (2.5,-5.5)\) and \((-4.75, 0.25)\).

George Birkhoff’s axioms are called metric because they assume the field axioms for real numbers; those of David Hilbert and myself are called intrinsic because they do not. Birkhoff is assuming tape measures longer than one’s work space that do not droop and protractors that measure angles to such precision that they can be projected across one’s work space and the opposite side of the triangle is as accurate as can be measured with one’s tape. Carpenters have no means of measuring angles with such precision and their tapes are only 25' long. The so-called Egyptian triangle can verify that an angle is right, but it does not create a right angle. Finding the corners of a rectangle can be frustrating for carpenters who know only this. It works only if the sides are rigid and reach across the entire work space, so there is no extrapolation error. The only time I recommend that construction workers use the Egyptian triangle is if they build an 8' wall, nail it to the floor, measure 6' from it, and then have two men stretch a tape diagonally; when their tape measures 10', nail the wall to the ceiling joists. It’s vertical!

Problem 1.17 Make a 16’ square cabin exactly square.

Solution Illustration
To make the cabin face south, stand at the SW corner and aim 45° minus magnetic declination off magnetic north; e.g. in Los Angeles, aim for 33° east. Lay off the diagonal, 22’ 7.5”, in this orientation. Have a man at each stake hold the end of a tape measure while you stretch them out to 16’ and pound stakes in where they intersect.

Squaring a 16' cabin is easy, but a rectangle with sides longer than a tape measure requires green-belt geometry. No construction worker has ever survived the green-belt entrance exam, so I will here break my vow against using unproven theorems and just present a cook-book recipe. A string can be extended six times longer than a tape measure and, because it is light weight, it does not droop when stretched across these long distances. Because a rectangle may be several times longer than your tape measure, you will need two strings in addition to your tape. Use a spring scale to put uniform tension on the string, about one Newton (100 grams) per meter.

Squaring a foundation must be achieved with no auxiliary lines outside it. This is because it may be in a hole if it is for a basement, or it may be surrounded by trees or cliffs if a plot of land was cleared and graded for a house being built in a forest or cut into a hillside. To make the house face a road, give the front the same compass heading as the center line of the road. To make the house face south, stand at the SW corner and aim 90° minus magnetic declination off magnetic north; e.g. in Los Angeles, aim for 78° east. Note that this is a Euclidean construction.

Problem 1.12
Square a house’s foundation before pouring the concrete floor.

Solution
Mark the front segment, \(\overline{EF}\), with two stakes measured with a tape and oriented with a compass to be parallel to a road or to the east-west line; do not neglect declination. Loop the end of string S₁ over the E-stake, stretch it across the front and tie it to the F-stake. Drive a stake, O , into the ground near the center, but slightly towards the front and slightly towards the -stake. Loop the end of string S₂ over the O-stake, stretch it to the F-stake, pinch it with your fingers and then swing this radius around the O-stake until the arc intersects \(\overline{EF}\). Celebrate the construction of an isosceles triangle by driving in another stake at this intersection, E₁. Do not lose your pinched-off length! Lift the S₁ string off the E-stake and loop it over the E₁-stake. Stretch it over and past the center stake, O; simultaneously, swing string S₂ around the o-stake to point in the opposite direction, away from E₁. Stretch both strings so they coincide (lie on top of each other) and drive a stake,G₁, in at the end of the length pinched-off on S₁. \(\angle E_{1}F_{1}G_{1}\) is right. Loop the end of string S₁ over the F-stake, stretch it into ray \(\overrightarrow{FG1}\) and drive a stake G on this ray past G₁ to where a tape measures the length of the side of the house. Pinch off this length, \(\overline{FG}\) , lift the S₁ string off the E-stake and loop it over the F-stake. Lift the S₂ string off the O-stake, loop it over the F-stake, pinch off the length \(\overline{EF}\), then lift it off the F-stake and loop it over the G-stake. Stretch both strings out and where their pinched off lengths intersect, drive a stake, H . \(\overline{EFGH}\) is a rectangle of the house’s dimensions.

This may seem complicated, but it leads directly to a rectangle while the Pythagorean theorem converse (if ,\(u^{2}+v^{2}=w^{2}\) then the triangle with these sides is right) is hit and miss. Purists are pulling out their hair because P. 1.17 and P. 1.18 are blue- and green-belt. But we must help the carpenters – We’re not just for mathletes! – and no carpenter has ever survived orange belt.

Many come to Geometry–Do with prejudice against deductive logic. Now is the time to rid ourselves of these losers! They are baggage we will not need to bring to yellow-belt geometry. Put construction workers and others who come to geometry with an open mind on Team Euclid. Put those who have closed their minds to deductive logic and believe only in coordinate geometry on Team Prástaro. In two classrooms, push the desks to the corners, staple butcher paper to the ceiling and draw a chalk line on it. Give each team a yardstick, two spools of chalked string and two ladders. A team that can draw a chalk line on the floor directly underneath the one on the ceiling gets an A, else an F. Test their answers with a plumb bob. If the losers on Team Prástaro demand a tape measure instead of a yard stick, explain that, unless you are building an outdoor toilet, rulers are always less than the length of one’s work space.

In the preceding section I wrote, “Finding the corners of a rectangle can be frustrating for carpenters who know only this.” So true! I remember when I was eight that my father had my mother, my brother and I at stakes marking three corners of the foundation of the basement for our house. He kept measuring sides one at a time with his only tape measure and ordering a stake moved a few inches this way or that. The Pythagorean theorem never came out exact and it offered no hints on how to move the stakes to make it exact. Bad day!

In Volume Two: Geometry with Multiplication, the Pythagorean theorem will be expressed as \(u^{2}+v^{2}=w^{2}\) with \(u,v,w\) being real numbers. However, real numbers were only introduced in the 1800s and the modern theory of rational numbers did not precede them by much. Yet Egyptologists assure us that triangles with sides of 3,4 and 5 units appear in four-thousand-year-old hieroglyphics. We will do the ancient proof and, in Volume Two, we will do it rigorously.

Egyptian Triangle Theorem
A triangle with sides three, four and five times a unit length is right.

Proof Illustration
By C. 1.3, raise a perpendicular from the endpoint of a segment. Quadrisect the segment and lay off three of these units on the perpendicular. Connect the endpoints and lay off these units on it. Observe that it takes exactly five units to fill it.

An analogous proof shows that a triangle of sides 5,12 and 13 is right; this was unknown to the Egyptians. Plumbers can use this triangle when installing 22.5° elbows. Integer solutions to the Pythagorean theorem are known as Pythagorean triples. Students should be aware that Euclid devised a formula that generates Pythagorean triples:\(u=m^{2}-n^{2}\),\(v=2mn\),\(u=m^{2}+n^{2}\) for positive integers \(m>n\). Verification is basic algebra; that \(ku,kv,kw\) for k=1,2.. gets them all is advanced. Try it with n=1 and m even, or n=2 and m odd. Know that Fermat’s Last Theorem states that there are no integer solutions to \(u^{n}+v^{n}=w^{n}\) for integers n>2.

\(3–4–5\) right triangles are ubiquitous in Common Core because the computer programmers who compose their exams want to keep things neat by using only integers. Varsity Tutors Advanced Geometry Exam, problem #22 gives a rhombus of sides 5 inscribed in a rectangle with height 4 and asks the area. Problem 1.16 is the \(3–4–5\) right triangle scaled up threefold and joined to the \(5–12–13\) right triangle to be a \(13–14–15\) triangle. A \(13–20–21\) triangle has a 12-unit altitude for the same reason. A \(15–20–25\) triangle is right – it’s the \(3–4–5\) triangle scaled up fivefold – and it is the threefold and fourfold \(3–4–5\) triangles joined along a 12-unit altitude; thus, it is the standard example of the geometric mean. These ubiquitous triangles all have integer areas.

As a geometer, you may be asked to design structures like gates, towers, gantries or bridges.

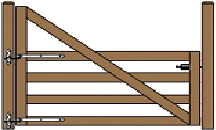
Wrong!

Everybody knows that a diagonal is required to make a rigid triangle, but a drive through the country indicates that few know which way it goes. Wood beams can withstand a tremendous compressive load – 1700 psi for Douglas Fir – but cannot lift a load because the screws pull out. Steel is just the opposite; \(\frac{1}{8}”\); wire rope can lift 340 pounds, but stainless-steel tubes kink and fold over under any large compressive load.

Wooden diagonals go from the foot of the gate post upwards and wire rope diagonals go from the top of the gate post downwards. For a wooden tower to be rigid it must have crossed wooden diagonals so there are some that are angled upwards towards any direction of wind.

A gantry is two A-frames with a beam between them and a hoist that slides along the beam. Mimicking the all-steel commercial ones with wood does not work because, when overloaded, the legs spread apart and bow outwards. The crossbar is pulling them together, which is not what wood does well. Put the crossbar at the midpoints of the legs, which is where they bow the most, and then squeeze the A-frame by running wire rope from each foot to where the crossbar meets the other leg. The beam should also be squeezed by guy wires staked to the ground on either side, going over the top of the beam and then being attached to the opposite A-frame.

A drive through the country indicates that almost all wooden gates have collapsed. This is because they have a wooden diagonal angled downwards and it reaches across the entire 12’ or 14’ gate, making too horizontal an angle. Also, failed gates were over-engineered on the latch side, adding unnecessary weight far from the hinges. 1” planks are all it takes to stop cattle.

The gate shown on the next page is 14’ wide for farm equipment and is designed to stop cattle, not people. The wire rope loops through the eyes and around both sides of the gate. Solid lines are 2”-thick boards or 4”-thick posts, dashed lines are 1”-thick planks. Note that the boards and posts are all assembled edgewise, so their widest sides are coplanar.

The C boards are inset into B and glued with wooden dowels to add strength. There are five hinges and the gate post is rectangular; two hinges attached to a round post are weak. In the winter the ground freezes to the frost line and, in the spring, the top few inches thaw but do not drain through the frozen ground below, which is why it is so muddy. Water that soaks into the gate post can only drain out the bottom if it extends below the frost line. Also, there should be gravel, not concrete, below it to aid drainage. Gates often collapse because the post rots.

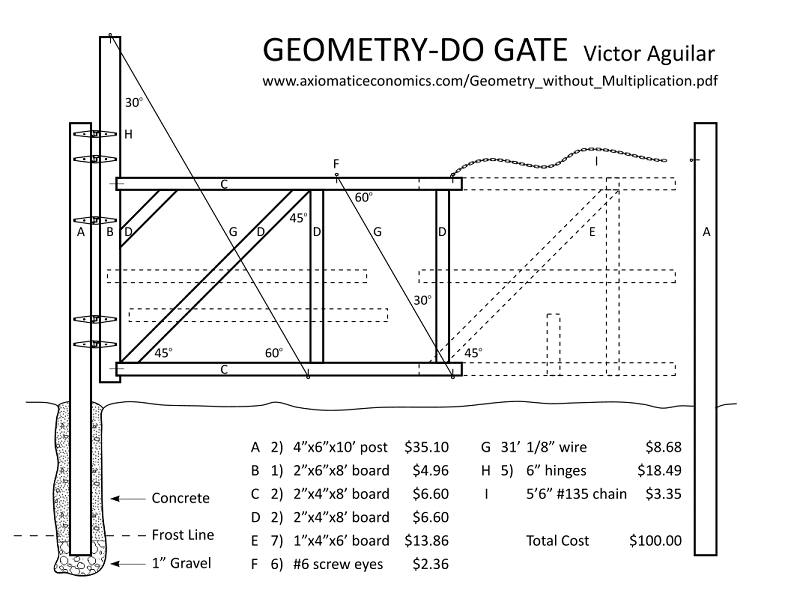
For automotive bridges too high to be supported with pillars, put a 4” x 6” x 12’ post vertical and two 4” x 4” posts at 45 under the center of each of the two stringers and lift them with 0.5” steel cables attached to eye bolts in the concrete footers. The two vertical posts should have crossed braces – it is a mistake to look only at the side view and neglect twisting forces.Yellow belts will learn to build stone bridges cut from river rocks that are strong enough to support truck traffic!

Detailed plans for wooden foot bridges of various sizes are available. Sorry Grasshopper, but, while the plans are free, the hula girl coming out to dance on your completed bridge is extra.

Steel cannons with rifled bores brought an end to state-sponsored castle construction, but some of what was learned during the time of smoothbore bronze cannons is still relevant today for people engaged in low-intensity conflicts¹⁰. By low-intensity I mean, by mutual consent, both the home owners and the bandits restrict themselves to small arms, usually defined as 7.62 mm rifles and hand grenades, because they are under a real army, but it will ignore small-arms fire.

The first principal of building fortifications is to build them for yourself, not for the enemy. If you dig trenches or set out some Jersey barriers, they may stop the enemy’s wheeled vehicles, but they will also provide cover for enemy infantry. Thus, you should have a vertical retaining wall facing rearward and an earthen glacis slope facing forward. Flatten the top of a gently rounded hill, digging deep enough that the cut-down area requires a three- to four-foot high retaining wall all around it. The windows are high enough that the defenders can graze the slope with rifle fire, but the attackers cannot fire at the base of the house wall until they crest the retaining wall.

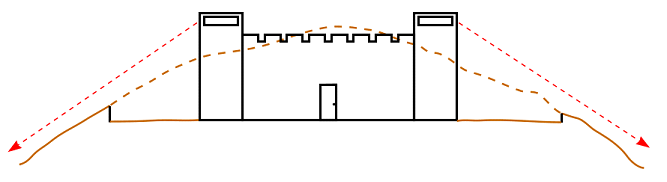
The second principal is to not have blind spots. The defenders should have bastions protruding from the corners of the building so attackers cannot press themselves up against the wall and be hidden from the windows. But, if the bastions are round, like the turrets in a medieval castle, there are blind spots directly in front of them. They should be tapered, like the points on a star.

The third principal is that stone shatters when hit by bullets, but concrete and brick do not. Also, landscape with crushed stone to make walking noisy. Get rid of boulders that can be thrown.

There is little application for geometry in the design of fortifications, but white-belt geometers should be familiar with the basics. Green belts will learn of machine gun emplacement, which really does require geometry. It would be embarrassing for the Geometry–Do practitioner to boast of these advanced techniques while showing ignorance of basics like glacis slopes.

Angle–Side–Angle (ASA) Theorem
Given two angles and the included side, a triangle is fully defined.

Proof
Given \(\overline{EFG}\) and \(\overline{HIJ}\) with \(\angle GEF=\angle JHI\), \(\overline{EF}=\overline{HI}\) and \(\angle EFG=\angle HIJ\), let us assume that \(\overline{GE} and \overline{JH}\) are not equal. Suppose that \(\overline{GE}>\overline{JH}\). By the interior angle axiom, there is a point K between G and E such that \(\overline{KE}=\overline{JH}\). \(\overline{EFK}\cong\overline{HIJ}\) by SAS and, by congruence, \(\angle EFK=\angle HIJ\). But \(\angle EFK<\angle EFG\) because K is inside \(\angle EFG\), which is given to be equal to \(\angle HIJ\); a contradiction. Suppose that \(\overline{GE}<\overline{JH}\). Proof that this is impossible is the same but has K between J and H. Thus, \(\overline{GE}=\overline{JH}\) and, by SAS, \(\overline{EFG}\cong\overline{HIJ}\). .

It is an easy corollary that isosceles triangles have two angle bisectors equal. Prove it, please.

Isosceles Triangle Theorem Converse
If two angles of a triangle are equal, then the opposite sides are equal.

Proof
Given \(\overline{EFG}\) with \(\angle E=\angle F\), \(\overline{EFG}\cong\overline{FEG}\) by ASA and thus \(\overline{GE}=\overline{GF}\)

Vertical Angles Theorem
Given \(\overleftrightarrow{EF}\) and \(G\), \(J\) on opposite sides of it, \(G\),\(E\),\(J\) are collinear iff a pair of vertical angles is equal.

Proof
Assume G, E, J are collinear in this order and F, E, K are collinear in this order. Then, \(\angle GEF\) and \(\angle GEK\) are supplementary. \(\angle GEJ\) is straight; thus, \(\angle GEF\) and \(\angle JEF\) are supplementary. \(\angle GEK\) and \(\angle JEF\) are both supplementary to \(\angle GEF\) and thus equal.

Assume F, E, K are collinear in this order; also, \(\angle GEK=\angle JEF\). F,E,K are collinear and thus \(\angle GEK\) and \(\angle GEF\) are supplementary. By substitution, \(\angle JEF\) and \(\angle GEF\) are supplementary; hence, G, E, J are collinear.

Exterior Angle Inequality Theorem
The exterior angle of a triangle is greater than either remote interior angle.
Given \(\overline{EFG}\), extend \(\overline{EF}\) to J. We must prove that 1) \(\angle EGF < \angle JFG\) and 2) \(\angle GEF < \angle JFG\) .

Proof
Bisect \(\overline{FG}\) at \(\overline{M_{FG}}\) and extend the median past \(\overline{M_{FG}}\) to double its length at K. Connect F and K. \(\angle KFM_{FG} < \angle JFM_{FG}\) because \(\angle JFK+\angle KFM_{FG}=\angle JFM_{FG}\). By the vertical angles theorem and SAS, \(\overline{GM_{FG}E}\cong\overline{FM_{FG}K}\), thus, \(\angle EGM_{FG}=\angle KFM_{FG}\). By substitution, \(\angle EGM_{FG}<\angle JFM_{FG}\) thus \(\angle EGF<\angle JFG\)

Proof of part two, that \(\angle GEF < \angle JFG\), is left as an exercise. Just bisect \(\overline{FE}\) instead of \(\overline{FG}\)

Greater Angle Theorem
If two sides of a triangle are unequal, then their opposite angles are unequal, the shorter side opposite the smaller angle and the longer side opposite the larger angle.

Proof
Given \(\overline{FG}<\overline{EF}\) in triangle \(\overline{EFG}\), find J between E and F such that \(\overline{HF}=\overline{FG}\) and connect it to G. By the Exterior Angle Inequality Theorem, \(\overline{FEG}<\overline{FJG}\). By the isosceles triangle theorem, \(\angle FJG=\angle FGJ\). Also, \(\angle FGJ<\angle FGE\) because the former is inside the latter. Thus, \(\angle FEG<\angle FJG=\angle FGJ<\angle FGE\). Simplifying, \(\angle FEG<\angle FGE\).

Greater Side Theorem
If two angles of a triangle are unequal, then their opposite sides are unequal, the smaller angle opposite the shorter side and the larger angle opposite the longer side.

The word angle or side in the name refers to the result, not the given information.

Triangle Inequality Theorem
Any side of a triangle is shorter than the sum of the other two sides.

As discussed in the Note to Philosophers, this is a direct result of the definition of a segment. It can also be proven using the greater angle and greater side theorems, as can the hinge theorem. A corollary is that diameters are the greatest chords. (They try not to let it go to their heads.)

Triangle Inequality Theorem Corollaries
1. Any side of a triangle is greater than the difference of the other two sides.
2. Given \(\overline{EFG}\) and P inside it, \(\overline{EP}+\overline{PF}< \overline{EG}+\overline{GF}\).
3. Given P not on \(\overleftrightarrow{EF}\) and \(P'\) its perpendicular foot on \(\overleftrightarrow{EF}\), if \(\overline{P'E}<\overline{P'F}\), then \(\overline{PE}<\overline{PF}\).

Hinge Theorem
Given two triangles with two corresponding sides equal, the included angle in one is smaller than in the other if and only if the opposite side is shorter in the former than in the latter.

Some geometers cite the triangle inequality theorem where I say “by definition of segments.” It is easier to define a segment as the shortest path between two points than to draw triangles among noncollinear points. Problems 2.3 and 2.5 are examples of this method. Shortest path has to be intuitive because, until Volume Two, we cannot associate real numbers with lengths.

Orange belts study parallel lines, which are everywhere equidistant. For this statement to mean something, we must define the distance from a point to a line. There are many points on a line that define segments to a point not on the line. Which segment? The one of minimum length!

Perpendicular Length Theorem
The perpendicular is unique and is the shortest segment from a point to a line.

Part One
There is only one segment from a point to a line that is perpendicular to it.

Proof
Drop a perpendicular from G to \(\overleftrightarrow{EF}\). Label the intersection G' and extend the perpendicular that much again to \(G_{EF}\). Let J be on \(\overleftrightarrow{EF}\) and not G'. By SAS, \(\overline{GG'J}\cong\overline{G_{EF}G'J}\) and, by congruence, \(\angle GJG'=\angle G_{EF}JG'\). By the segment postulate, \(\angle GJG_{EF}\) is not a straight angle because \(\angle GG'G_{EF}\) is straight and two points fully define a segment. If \(\angle GJG_{EF}\) is not straight, then \(\angle GJG'\), which is half of \(\angle GJG_{EF}\), is not right.

Dropping a perpendicular uses C. 1.1, extending a segment uses the line segment postulate and adding an equal segment uses addition. Thus, SAS means that \(\overline{GG'}=\overline{G_{EF}G'}\), \(\angle GG'J=\angle G_{EF}G'J\) by the right angle postulate, and \(\overline{G'J}=\overline{G'J}\) by reflexivity. All of this is omitted for the sake of brevity.

Part Two
The perpendicular is the shortest segment from a point to a line.

Proof
\(\overline{GG_{EF}}<\overline{GJ}+\overline{JG_{EF}}\) by the triangle inequality theorem. \(\overline{GG'J}\cong\overline{G_{EF}G'J}\) holds the equality \(\overline{GJ}+\overline{JG_{EF}}\). Halve both sides of \(\overline{GG_{EF}}<\overline{GJ}+\overline{JG_{EF}}\) so \(\overline{GG'}<\overline{GJ}\).

It is an easy corollary that two distinct perpendiculars raised from a line never intersect.

Angle–Angle–Side (AAS) Theorem
Given two angles and a side opposite one of them, a triangle is fully defined.

Proof
Given \(\overline{EFG}\) and \(\overline{JKL}\) with \(\angle E=\angle J, \angle F=\angle K\) and \(\overline{FG}=\overline{KL}\), assume that \(\overline{EF}\) and \(\overline{JK}\) are not equal; Suppose, that \(\overline{JK}<\overline{EF}\). Thus, there is a M between E and F such that \(\overline{MF}=\overline{JK}\). \(\overline{MFG}\cong\overline{JKL}\) By SAS, so \(\overline{GMF}=\overline{LJK}\). But \(\angle LJK=\angle GEF\) is given, so \(\angle GMF=\angle GEF\). \(\angle GMF\) is an exterior angle of \(\overline{EMG}\) equal to a remote interior angle of \(\overline{EMG}\), which contradicts the Exterior Angle Inequality Theorem. Thus, the assumption that \(\overline{JK}<\overline{EF}\) is not be true. Analogously \(\overline{EF}<\overline{JK}\) is not true. By trichotomy \(\overline{EF}=\overline{JK}\)SAS, \(\overline{EFG}\cong\overline{JKL}\).

Isosceles Altitudes Theorem
Two altitudes are equal if and only if the triangle is isosceles.

Proof
Given \(\overline{EFG}\), assume that \(\overline{EG}=\overline{FG}\). By AAS, \(\overline{E'GE}\cong\overline{F'GF}\), so \(\overline{E'E}=\overline{F'F}\).

Given \(\overline{EFG}\), assume that \(\overline{E'E}=\overline{F'F}\). By AAS, \(\overline{GE'E}\cong\overline{GF'F}\), so \(\overline{GE}=\overline{GF}\).

This is easy, but it is instructive in two ways: First, it is bi-conditional and illustrates that the two implications are proven independently, each assuming one statement and then using it to prove the other statement. Second, it illustrates the importance of ordering the vertices correctly.

Hypotenuse–Leg (HL) Theorem
Given the hypotenuse and one leg of a right triangle, it is fully defined.

Proof
By C. 1.3, raise a perpendicular from a line the length of the leg and connect its endpoint to the line on both sides with segments the length of the hypotenuse. By the isosceles triangle theorem, the base angles are equal, and by AAS, the triangles are congruent.

Viviani Midpoint Theorem
A triangle is isosceles iff perpendiculars dropped from the base midpoint onto the sides are equal.

ASS cannot be a congruence theorem because it lacks uniqueness. Even if \(\overline{EFG}\cong\overline{JKL}\), another triangle, \(\overline{EFG''}\), can be constructed with the same angle, side and side and it is not congruent to \(\overline{JKL}\). HL initially seems to lack uniqueness because we can construct two triangles, \(\overline{EFG}\) and \(\overline{EFG''}\), with \(\angle E\) right, \(\overline{EF}\) the leg and \(\overline{EG}=\overline{EG''}\) the hypotenuse. But \(\overline{EFG}\cong\overline{EFG''}\) and so we know that \(\overline{EFG}\cong\overline{JKL}\) if and only if \(\overline{EFG''}\cong\overline{JKL}\) because congruence is transitive.

Counter-Example to the ASS Congruence “Theorem”

Faced with tremulous home-school parents who intended to teach geometry using his textbook but were unsure that they could, Kiselev bolstered their courage by casting a magic spell on them:

Those reading these lines are hereby summoned to raise their children to a good command of Elementary Geometry, to be judged by the rigorous standards of the ancient Greek mathematicians.

You will be pleased or perhaps appalled to learn that I too can cast magic spells… actually curses. The Aguilar Curse: Students who try to use the ASS “theorem” will grow donkey ears.

Johnny Geometer claims that any point P on \(\overline{EF}\) bisects it! Let \(\overline{EG}=\overline{FG}\). \(\angle E=\angle F\) by the isosceles triangle theorem and \(\overline{PG}=\overline{PG}\) by reflexivity. By ASS, \(\overline{EGP}\cong\overline{FGP}\), so \(\overline{EP}=\overline{FP}\).

This completes the basic geometry that even lame-brain Common Core students learn. The difference is that we prove these theorems and, hence, they must be presented in the correct order. Common Core students are just given a jumble of stuff to memorize in no particular order. Now that we’ve got the basics, let’s use what we know to solve some practical problems!

Problem 2.1
Without a laser rangefinder, measure the distance across a river to construct a cable ferry.

Solution
If E and P are posts on opposite banks, find F inland of E and in line with \(\overleftrightarrow{EP}\). By P 1.18, construct a rectangle \overline{EFGH}. Find P1 on \(\overrightarrow{HG}\) such that one can sight on P directly over a flag at \(M_{EH}\). By ASA, \(\overline{EP}=\overline{HP_{1}}\), the length of cable needed.

This classic problem usually begins, “Construct \(\overline{EH}\bot\overline{EP}\)". But how, without the full rectangle? P 2.1 is yellow belt because we could use a transit, but P 1.18 is the inexpensive way to do it. (A transit is an optical device mounted on a tripod that measures angles. A theodolite is too, but more expensive.)

Problem 2.2
Use a transit to construct the corners of a house equidistant to a road concealed behind a fence.

Solution
Remove a plank or drill a hole in the fence roughly perpendicular to the middle of the house. At the corner post, sight through the hole to the road. Put the transit there and measure the acute angle with the road. Move the transit to the corner post and lay off this angle. By AAS, the front of the house is on this ray. Fix the hole in the fence.

Lemma 2.1
The sum of any two interior angles of a triangle is less than a straight angle.

Proof
Consider \(\angle E\) and \(\angle F\) in \(\overline{EFG}\) and let J be on the extension of \(\overline{EF}\) so \(\angle JFG\) is exterior to \(\angle EFG\). By the Exterior Angle Inequality Theorem, \(\angle FEG<\angle JFG\). By supplementarity, \(\angle EFG+\angle \overline{JFG} = \sigma \) and, by substitution, \(\angle EFG+\angle FEG < \sigma\).

This lemma is absolute geometry in the sense that Bolyai used the term to mean what is common to Euclidean and hyperbolic geometry. But it is not true in elliptic geometry. Some people use the term to include all three geometries. We will use the term in Bolyai’s sense.

Angle–Side–Longer Side (ASL) Theorem
Given an angle and the side opposite the angle not less than a near side, a triangle is fully defined.

Proof
Given \(\overline{EFG}\) and \(\overline{JKL}\) with \(\angle E=\angle J, \overline{EF}=\overline{JK}\) and \(\overline{FG}=\overline{KL}\), assume that \(\overline{JL}\neq\overline{EG}\); specifically, that \(\overline{JL}<\overline{EG}\). Thus, there is a M between E and G such that \(\overline{EM}=\overline{JL}\). By SAS, \(\overline{EFM}\cong\overline{JKL}\), which holds the equality \(\overline{FM}=\overline{KL}\). But \(\overline{FG}=\overline{KL}\) is given, so \(\overline{FM}=\overline{KL}\) by transitivity and \(\angle FMG=\angle FGM\) by the isosceles triangle theorem. By lemma 2.1, their sum is less than a straight angle and, since they are equal, they are acute; hence, \(\angle EMF\) is obtuse by supplementarity. By lemma 2.1, \(\angle EMF\) is larger than both \(\angle MEF\) and \(\angle MFE\) because together they must sum to an acute angle. By the greater side theorem, \(\overline{EF}\) is the longest side, which contradicts the assumption that the side opposite \(\angle E\) is longer than it. Thus, the assumption \(\overline{JL}\neq\overline{EG}\) is wrong. by SSS \(\overline{EFG}\cong\overline{JKL}\)

Given \(\overline{EFG}\) and \(\overline{JKL}\) with \(\angle E=\angle J\), \(\overline{EF}=\overline{JK}\) and \(\overline{FG}=\overline{KL}\), if \(\angle G\) and \(\angle L\) are both obtuse, right or acute, then \(\overline{EFG}\cong\overline{JKL}\). This is an alternative way to state the ASL Theorem. Next is OSS, a corollary of ASL that is cited in the classic proof of the Steiner-Lehmus theorem. It states that ASS works for obtuse triangles.

Obtuse Angle–Side–Side (OSS) Theorem
Given an obtuse angle and two sides that are not bracketing it, a triangle is fully defined.

Proof citing ASL
By lemma 2.1, the obtuse angle is larger than either of the other angles so, by the greater side theorem, the side opposite it is longer than either other side. Thus, by ASL.

Proof citing HL
By supplementarity, the angle exterior to the given angle is fully defined. Drop a perpendicular from the vertex between the given sides to the extension of the unknown side. It intersects the extension because the given angle is obtuse and forms a triangle outside the given triangle that, by AAS, fully defines the length of the altitude. By HL, the union of the two triangles is fully defined and, by subtraction, the given one is.

We now prove a fundamental theorem that will be cited throughout, and then some theorems about circles that do not cite any version of the parallel postulate. Thus, potential students of non-Euclidean geometry can read the white- and yellow-belt chapters without learning of any theorems (except ASL, which contradicts elliptic geometry) that will contradict their later studies.

Angle Bisector Theorem
A point is on an angle bisector if and only if it is equidistant from the sides of the angle.

Proof
Given the angle bisection, the point is equidistant by AAS; the converse by HL.

Chords Inside Circles Theorem
Chords are inside their circle.

Proof
Let \(M\) be inside chord \(\overline{EF}\), center \(O\). \(\angle OEM=\angle OFM\) by the isosceles triangle theorem. \(\angle OMF>\angle OEM\) by the greater angle theorem, so \(\angle OMF>\angle OFM\) and, by the greater side theorem, \(\overline{OF}>\overline{OM}\); that is, \(M\) is closer to the center than a point on the circle.

Diameter and Chord Theorem
A diameter bisects a chord if and only if the diameter is perpendicular to the chord.

Proof
If a diameter bisects the chord, then, by SSS, the two triangles formed by connecting radii to the endpoints of the chord are congruent and, by the mediator theorem, the diameter is perpendicular to the chord. Suppose the diameter is perpendicular to the chord; by HL, the two triangles to either side of it are congruent and the chord is bisected.

Diameter and Chord Theorem Corollary
Given a circle with center \(O\) and \(E, F, T\) on the circle such that \(\overleftrightarrow{EF}\bot\overleftrightarrow{OT}\), then \(\overline{ET}=\overline{FT}\)

Equal Chords Theorem
In the same or equal circles, equal chords are equally distant from the center, and the converse.

Proof
Suppose the chords are equal. Draw radii to the endpoints and drop perpendiculars from the center to the chords. By the diameter and chord theorem, these perpendiculars bisect the chords and thus the half chords are equal. By HL, the half triangles are congruent and so the distances from the chords to the center are equal

Proof of the converse is left as an exercise.

Common Chord Theorem
If two circles have a common chord, its mediator is the line of centers.

Proof
By the diameter and chord theorem, the mediator of the chord is a diameter to both circles and on the line of centers.

The common chord theorem is also true if the chord is reduced in length to a point. If two circles touch at a single point they are tangent; they may be side-by-side or one inside the other.

Lemma 2.2
A line intersects a circle in at most two points.

Proof
Let E, F, G be intersection points of a line and a circle with F inside \(\overline{EG}\). E and G are on the circle, so \(\overline{EG}\) is a chord. By the chords inside circles theorem, F is inside the circle.

Tangent Theorem
A line intersects a circle where it is perpendicular to the radius iff that is a point of tangency.

Proof
Let T be a point of intersection perpendicular to the radius and O be the circle center. Suppose the line and the circle also intersect at S. Find U on the line such that \(\overline{ST}=\overline{TU}\). By the SAS, \(\overline{SU}\cong\overline{UTO}\) so \(\overline{SO}=\overline{UO}\). U is on the circle. Thus, \(S, T, U\) are distinct points on a line and also on a circle, a contradiction by lemma 2.2, so T is a point of tangency.

Assume that the line intersects only once; every other point on the line is outside the circle and thus farther from the center than the radius. By the perpendicular length theorem, only the perpendicular is the shortest segment from a point to a line.

Construction 2.1
Through a point outside a circle, draw a line tangent to the circle.

Yellow Belt Solution
Let O be the center of the given circle, P be the given point and M be the intersection of \(\overline{OP}\) with the circle. Draw a concentric circle that passes through \(P\). By C. 1.3, raise a perpendicular from \(M\) and call its intersection with the larger circle \(Q\). Let \(T\) be the intersection of \(\overline{OQ}\) and the given circle; \(T\) is the desired tangent point.

Proof
By SAS, \(\overline{MOQ}\cong\overline{TOP}\), which holds the equality \(\angle M=\angle T. \angle M\) is right by construction, so \(\angle T\) is right and, by the tangent theorem, \(T\) is a tangent point.

When the point is far from the circle (e.g. a machine gun and its kill circle), the outer circle may go over the edge of the paper. Also, one’s compass may not be large enough to draw this big circle. The green-belt solution requires an arc only half this radius and extending no farther than the given circle, so it will be the standard technique. But, even if yellow belts do not have the most efficient method, they have a method, so everything we describe in this chapter is feasible.

Common Point Theorem
An intersection of two circles is a tangent point if and only if it is on the line of centers.

Proof
If it is a tangent point, then, by the tangent theorem, it is perpendicular to the radii from both centers and, by supplementarity, it is on the line of centers. If it is on the line of centers, then, by the perpendicular length theorem, the tangent there is unique.

This theorem is like the common chord theorem but for circles that just touch. It is needed by construction workers who wish to blend arcs smoothly together; e.g. for concrete curbs that partition flower beds. An asphalt company might use this theorem to pave an S-shaped driveway to a detached garage. Orange Belt Geometry for Construction Workers uses this theorem to prove that the haunch and the crown arcs of a Tudor or generic arch blend smoothly together.

Two Tangents Theorem
Two tangents from an external point are equal and their angle bisector intersects the center.

Proof
By the tangent theorem, the points of tangency are where the radii are perpendicular to the tangents and so, by the perpendicular length theorem, the center is equidistant from the tangents. By the angle bisector theorem , their angle bisector intersects the center and, by HL, the two triangles are congruent. Hence, the tangents are equal.

Tangent Bisection Theorem I
If two circles touch, the perpendicular to the line of centers through the circles’ touching point cuts their common tangents in half.

Blue belts will prove tangent bisection theorem II about the extension of the common chord.

Mirror Problem
Find the point on a mirror to shine a laser at a target.

Solution
Let \(L\) be the light and \(T\) be the observer. Drop a perpendicular from \(L\) and \(T\) to the mirror or its extension with feet \(L'\) and \(T'\).Extend \(\overline{TT'}\) an equal distance to \(T_{L'T'}\). Define \(T_{L'T'}\) as the reflection of \(T\) about the line \(\overleftrightarrow{L'T'}\). Let \(P\)=\(\overline{LT_{L'T'}}\cap\overleftrightarrow{L'T'}\) By SAS, \(\overline{TT'P}\cong\overline{T_{L'T'}T'P}\), so \(\angle TPT'=\angle T_{L'T'}PT'\). by the Vertical Angles Theorem \(\overline{T_{L'T'}PT'}\cong\overline{LPL'}\). By transivity, \(\angle TPT'=\angle LPL'\), sp P is aiming point.

A reflection is a point defined by another point and a line; the target is the reflection of the point behind the mirror that the laser is aimed at, and vice-versa. Because the two points are the same distance from the mirror, reflection is an isometry; a transformation that preserves distance. \(M_{EF}, M_{FG}, M_{EG}\) are midpoints; in a tangential quadrilateral, \(I_{EF}, I_{FG}, I_{GH}, I_{HE}\) are incircle touching points. These and Thébault’s notation are exceptions to double subscripts denoting reflections.

Problem 2.3
We wish to pound an anchor between two poles with guy wires to the tops of each pole to reinforce them. Where should we position the anchor to use the shortest possible wire?

Solution
Guess at where the anchor should be and draw in the guy wires. Draw a guy wire to one pole’s reflection. By SAS the reflected triangles are congruent and so their hypotenuses are equal. By definition of segment, if the anchor is not collinear with the end of one pole and the end of the other pole’s reflection, it is badly guessed. Correct it.

The guy wire is a physical representation of a light beam. Thus, the mirror property is that reflections preserve distance, so the light beam in the mirror problem travels the same distance if it bounces off the mirror to the observer or if it penetrates and goes to the observer’s reflection.

Problem 2.4
From a house in the country, construct a dirt road to a straight paved road, the latter twice as fast as the former, to minimize travel time to a nearby town on the paved road.

Solution
Guess at where the intersection should be. On the other side of the paved road, construct a half equilateral triangle with the hypotenuse on the paved road to town and the short leg extending into the dirt. From the intersection, you could get to the right angle or to town in the same time. By definition of segment, if the intersection is not collinear with the house and the right triangle, it is badly guessed. Correct it.

This is an important lesson, Grasshopper. If asked to minimize the sum of segments that are not collinear, use congruence theorems to show that this is equal to the sum of segments that can be made collinear. By the definition of segment, the shortest path has all straight joints. We guessed at the answer, drew a figure, saw what was wrong with the guess and then corrected it.

Problem 2.5
Given \(\angle EFG\) and \(P\) within it, find points on each ray such that the perimeter of the triangle they make with \(P\) is minimal.

Solution
Let \(P_{FE}\) and \(P_{FG}\) be reflections of P about \(\overrightarrow{FE}\) and \(\overrightarrow{FG}\) respectively. Let \(J=\overline{P_{FE}P_{FG}}\cap\overrightarrow{FE}\) and \(K=\overline{P_{FE}P_{FG}}\cap\overrightarrow{FE}\). \(\overline{PJK}\) has perimeter \(\overline{P_{FE}P_{FG}}\), which is of minimal length.

Constructing a triangle so its perimeter is minimal will become the bread and butter of the Geometry–Do practitioner; he should be able to just look at a problem like P. 2.5 and immediately construct the solution. But the thought process of guessing at the solution and then seeing what is wrong with the picture so it can be redrawn correctly should not be forgotten. (Here, if we had guessed at \(J\) and \(K\), then drawn \(\overleftrightarrow{JK}\), laid off \(\overline{PJ}\) past \(J\) to \(P_{FE}\) and laid off \(\overline{PK}\) past \(K\) to \(P_{FG}\), our “solution” would violate the perpendicular length theorem.) If the student becomes too blasé about the initially easy problems, he will later encounter a difficult problem and feel like he has run into a wall. But, if he thinks carefully on the easy problems and treats each one as training for more difficult problems that he knows are coming, he will later discover himself doing problems that other geometers consider difficult without having ever noticed his own passage.

If the student becomes too blasé about the initially easy problems, he will later encounter a difficult problem and feel like he has run into a wall. But, if he thinks carefully on the easy problems and treats each one as training for more difficult problems that he knows are coming, he will later discover himself doing problems that other geometers consider difficult without having ever noticed his own passage.

Minimal Base Theorem
Given the apex angle and the sum of the legs, the triangle with minimal base is isosceles.

Proof
Given \(\overline{EFG}\) so \(\angle G\) is the given apex angle and \(\overline{GE}=\overline{GF}\), are each half the given sum of legs, Lay off a small but arbitary length \(x\) on \(\overrightarrow{GE}\) and subtract it from \(\overrightarrow{GF}\) to points \(J\) and \(K\), respectively. \(\overline{GE}+\overline{GF}=overline{GJ}+\overline{GK}\). Drop perpendiculars from \(J\) and \(K\) to \(\overleftrightarrow{EF}\) with feet \(J'\) and \(K'\), respectively. By the Isosceles Triangle Theorem Converse and the Vertical Angles Theorem, \(\angle J'EJ=\angle K'FK\). By AAS, \(\overline{J'EJ}\cong\overline{K'FK}\), so \(\overline{EF}=\overline{J'K'}\). But \(\overline{J'K'}<\overline{JK}\) by the triangle inequality theorem. Thus, \(\overline{EF}\) is the shortest possible base.

It is an easy corollary that the shortest chord through a point in a circle is perpendicular to the diameter through that point; this is how the theorem is sometimes stated in other textbooks.

Common Core textbooks are fond of the acronym CPCTC, which stands for Corresponding Parts of Congruent Triangles are Congruent. I do not use this acronym for two reasons:

1. It is wrong. It should be Corresponding Magnitudes of Congruent Triangles are Equal, or CMCTE. “Parts” is nowhere defined; they are magnitudes. Using the term congruent for both triangles and magnitudes to the complete exclusion of the term equal is wrong. Congruence and equality are different things; there is good cause for having two words.

2. It is excessively verbose. When I say, “by SAS, \(\overline{EFG}\cong\overline{JKL}\) and so \(\overline{GE}=\overline{LJ}\),” the students know immediately from how the vertices are ordered that \(\overline{EF}=\overline{JK}\) and \(\angle EFG=\angle JKL\) and \(\overline{FG}=\overline{KJ}\). Sometimes I will say, \(\overline{EFG}\cong\overline{JKL}\), which holds the equality \(\overline{EG}=\overline{JK}\).” Students know that we say that two triangles are congruent because congruence implies that corresponding magnitudes are equal; they do not need to be repetitively told this.

Problem 2.6
Through one of the two points of intersection of two equal circles, draw two equal chords, one in each circle, forming a given angle.

Solution
Bisect the given angle and replicate this on both sides of the common chord. The sides of this angle extended make two chords, one in each circle, forming the given angle.

If the angle goes between the centers, then the proof is easy because it can cite the vertical angles theorem. But we must take every possibility into consideration!

Proof
Let \(O_{1}, O_{2}\) be the centers, \(\overline{FG}\) their common chord and \(F_{1}, F_{2}\) the endpoints of the constructed chords \(FF_{1}, FF_{2}\) in circles around \(O_{1}, O_{2}\), respectively. By the Common Chord Theorem and HL, \(\overline{O_{1}FM_{FG}}\cong\overline{O_{2}FM_{FG}}\), and so \(\angle O_{1}FM_{FG}=\angle O_{2}FM_{FG}\). By angle addition, \(\angle F_{1}FG=\angle O_{1}FM_{FG}\pm\angle O_{1}FF_{1}\) and \(\angle F_{2}FG=\angle O_{2}FM_{FG}\pm\angle O_{2}FF_{2}\). By angle addition, \(\angle F_{1}FO_{1}=\angle F_{2}FO_{2}\). By the diameter and chord theorem, \(\angle O_{1}M_{F1F}F\) and \(\angle O_{2}M_{F2F}F\) are right. By AAS, \(\overline{M_{F1F}FO_{1}}\cong\overline{M_{F2F}FO_{2}}\), so \(\overline{M_{F1F}F}=\overline{M_{F2F}F}\). Doubling, \(\overline{FF_{1}=FF_{2}}\).

Wasn’t this proof made a lot easier by saying “and so” than by citing CMCTE? In How Math Can Be Taught Better, I mock a Common Core textbook that takes five steps to prove that two angles, both given as right, are equal. Duh! Common Core textbook authors purposefully make proofs as boring and tedious as possible, so nobody will lament their loss in the remaining 95% of the textbook when the author just starts announcing theorems without proving them. Clever! Let us now illustrate another method for solving geometry problems: Solve the problem with algebra and then replicate the algebra with geometry.

Construction 2.2
Construct two segments given their sum and their difference.

Solution
Add the sum and the difference. Bisect this to get the longer segment and then cut off the difference to get the shorter segment.

\((x+y)+(x-y)=2x\) Thus, we add the sum and the difference and then bisect it to get the longer side. \(x-(x-y)=y\) Thus, we cut off the difference to get the shorter segment.

For the most part I despise Common Core, but one practice that I will adopt is their insistence that math classes include some classic literature. Who hasn’t read The Pit and the Pendulum?

I could no longer doubt the doom prepared for me by monkish ingenuity in torture… [The pendulum’s] nether extremity was formed of a crescent of glittering steel, about a foot in length from horn to horn; the horns upward, and the under edge evidently as keen as that of a razor. - Edgar Allen Poe

Problem 2.7
If the horns of Poe’s pendulum are at points E and F one moment and then at points E' and F' a minute later, where is the axle from which the pendulum is suspended?

Solution
By the diameter and chord theorem, the mediators to chords \(\overline{EE'}\) and \(\overline{FF'}\) are diameters. Their intersection is the common center of the two concentric circles.

Note that \(\overline{EF}\) and \(\overline{E'F'}\) are not chords; there is no assurance that the horns rise equally above the blade. The endpoints of each chord are the same vertex of the figure at different times. Each point on the pendulum makes its own circle around an axle common to them all.

We next introduce our first triangle center! Other centers exist for acute triangles and, while we cannot define this precisely, for almost acute triangles, but they require the parallel postulate for general triangles. The medial point exists in absolute geometry, but it is deferred to orange belt.

Three highways cross farmland and intersect to form a triangle. People have complained that cell phone service is poor in this area, so the cell phone company intends to build a tower equidistant from the three highways. Where should they build it to best serve their customers?

Incenter Theorem
The bisectors of a triangle’s interior angles are concurrent at a point we will call the incenter.

Solution
By the angle bisector theorem, any point on the angle bisector of a vertex is equidistant from the sides, including the point where it intersects with the angle bisector of another vertex. This point, being on the angle bisector of the other vertex, is equidistant from the sides on either side of it. By transitivity, all three angle bisectors are concurrent.

The incircle is around the incenter and touches the sides at \(I_{E}, I_{F}, I_{G}\). The verb “inscribe” refers to drawing a circle in a triangle, never a triangle in a circle; this construction is not fully defined.

A city park is in the corner of two roads that intersect at an arbitrary angle; in this park, the VFW has erected a statue of a soldier and the city government has erected a statue of the town’s founder. They wish to split the cost of a flagpole and position it where it is equally visible to drivers on both roads, and it is also equidistant from their respective monuments. Where?

Problem 2.8
Given two points inside an angle, find a point equidistant from the points and from the rays.

Military cadets should know what the words enfilade and defilade mean. To enfilade a road or a trench is to fire down the length of it. This is important to machine gunners because it is difficult to traverse a gun to lead a moving vehicle; guns only work well if the enemy is coming directly at you or – even better – directly away from you. Also, this is the only way to get bullets inside a trench; firing across it is pointless. Thus, gunners will make use of C. 2.1 to locate their kill zone on a curved road or trench. Grenadiers can traverse their launch tubes more easily than heavy machine gunners, so they usually fire from defilade; that is, from a concealed position alongside a road. But their projectile is much slower than a bullet, so they need to get as close as possible. They use C. 1.1 to be equidistant from two roads to fire on either with the same calculated lead. The following theorem shows that an equilateral triangle with an important point at the center (e.g. a munitions dump) is the best defense against both enemy aircraft and enemy troops if you have only three anti-aircraft guns. This motivates the Dakota defense problem, to be solved later. In absolute geometry, the “circumscribe” exists for acute triangles, which is sufficient for the following theorem. The verb “circumscribe” always refers to drawing a circle around a triangle.

Incenter and Circumcenter Theorem
A triangle is equilateral if and only if its incenter and its circumcenter coincide.

Laying ambushes is great fun (unless, of course, you get killed), but we cannot immediately put heavy machine guns in the students’ hands. We have more geometry to learn, so let’s get busy!

Incircle Theorem
Given \(\overline{EFG}\), then twice \(\overline{I_{G}M_{EF}}\) is the difference of \(\overline{FG}\) and \(\overline{GE}\); that is, \(|\overline{FG}-\overline{GE}|\).

Proof
Assume \(\overline{FG}>\overline{GE}\); \(I_{G}\) is between E and \(M_{EF}\). If not, just re-label E and F. By segment addition, \(\overline{EI_{G}}+\overline{I_{G}M_{EF}}=\overline{EM_{EF}=M_{EF}F}=\overline{I_{G}F-I_{G}M_{EF}}\); thus, \(\overline{2I_{G}M_{EF}}=\overline{I_{G}F-EI_{G}}\).

\(\overline{2I_{G}M_{EF}}=\overline{I_{E}F}-\overline{EI_{F}}\)             Two Tangents Theorem
\(\overline{I_{E}F}-\overline{EI_{F}}\) + \(\overline{I_{E}G}-\overline{I_{E}G}\)         Two Tangents Theorem
\((\overline{I_{E}F}+\overline{I_{E}G})\) - \((\overline{EI_{F}+I_{E}G})\)     Additive group properties
\(\overline{FG}\)-\(\overline{GE}\)                                   Segment addition

Problem 2.9
Given \(\overline{EFG}\) with I the incenter, drop a perpendicular from E onto \(\overleftrightarrow{GI}\) with foot J and extend \(\overrightarrow{EJ}\) to K on \(\overline{FG}\). Prove that \(2I_{G}M_{EF}=\overline{FK}\).

Proof
Assume \(\overline{FG}>\overline{GE}\); if not, just re-label E and F. By ASA, \(\overline{GJK}\cong\overline{GJE}\), so \(\overline{GK}=\overline{GE}\).

\(2\overline{I_{G}M_{EF}}\)=\(\overline{FG}-\overline{GE}\)           Incircle theorem
\(=\overline{FK}+\overline{GK}-\overline{GE}\)           Segment addition
\(=\overline{FK}\)                                   \(\overline{GK}=\overline{GE}\)

Problem 2.10
given \(\overline{EFG}\) such that \(\overline{EF}<\overline{FG}<\overline{GE}\), then \(\overline{I_{E}M_{FG}}=\overline{I_{G}M_{EF}}+\overline{I_{F}M_{GE}}\).

Proof
\(2\overline{I_{G}M_{EF}}+2\overline{I_{F}M_{GE}} = \overline{GE}-\overline{FG}+\overline{FG}-\overline{EF} = \overline{GE}-\overline{EF} = 2\overline{I_{E}M_{FG}}\) by the incircle theorem. Halve both sides of the equation.

This one is easy to get confused in your mind. Just remember that the segment on the middling side of the triangle is equal to the sum of the segments on the short and long sides of the triangle.

Tangential Quadrilateral Theorem I
A quadrilateral is tangential if and only if any three of its angle bisectors are concurrent.

Proof
Given \(\overline{EFGH}\), assume that the angle bisectors of \(\angle E, \angle F, \angle G\) are concurrent at I, then three uses of the angle bisector theorem on \(\angle E, \angle F, \angle G\) prove I is equidistant to \(\overline{EF}\) and \(\overline{EH}\); also to \(\overline{FE}\) and \(\overline{FG}\); also to \(\overline{GF}\) and \(\overline{GH}.\) By transitivity, it is equidistant to all the sides.

Assume that \(\overline{EFGH}\) is tangential. By HL, \(\angle I_{HE}IE\cong\angle I_{EF}IE, so \angle I_{HE}EI=\angle I_{EF}EI\). Thus, I is on the angle bisector of \(\angle E\); analogously, I is on the angle bisectors of \(\angle F, \angle G, \angle H\).

Pitot Theorem
In a tangential quadrilateral, the sums of each pair of opposite sides are equal.

Proof
Let \(\overline{EFGH}\) be tangential and \(I_{EF}, I_{FG}, I_{GH}, I_{HE}\) be the incircle’s points of tangency. Then, \(\overline{EF}+\overline{GH}=\overline{EI_{EF}}+\overline{FI_{EF}}+\overline{GI_{GH}}+\overline{HI_{GH}}\). By the Two Tangents Theorem, \(\overline{EI_{EF}}=\overline{EI_{HE}}\) and \(\overline{FI_{EF}}=\overline{FI_{FG}}\) and \(\overline{GI_{GH}}=\overline{GI_{FG}}\) and \(\overline{HI_{GH}}=\overline{HI_{HE}}\) Thus, \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\).

Construction 2.3
Construct a rhombus; that is, a quadrilateral with all equal sides

Solution
Draw a segment of length \(r\), another at its endpoint at any angle and two circles of radius \(r\) around the extreme endpoints; their intersection is the fourth vertex.

Lemma 2.3
A rhombus is tangential.

The following standard textbook proof is Euclidean because it cites the circumcenter theorem.

Pitot Theorem Converse
If the sums of each pair of opposite sides of a quadrilateral are equal, it is tangential.

Euclidean Proof
Given \(\overline{EFGH}\) with \(\overline{EF}+\overline{GH}=\overline{EH}+\overline{GF}\), if all the sides are equal, the result by lemma 2.3. If not, then \(\overline{EH}<\overline{EF}\), or relabel so this is true. For the equality to hold, \(\overline{GH}<\overline{GF}\). Lay off \(\overline{EH}\) on \(\overline{EF}\) to J so \(\overline{EH}=\overline{EJ}\). Lay off \(\overline{GH}\) on \(\overline{GF}\) to K so \(\overline{GH}=\overline{GK}\). These sides are the bases of isosceles triangles \(\overline{HJE}, \overline{JKF}, \overline{KHG}\). By the center line theorem, the mediators of the sides of \(\overline{HJK}\) bisect \(\angle E, \angle F, \angle G\); by the circumcenter theorem, they are concurrent. By Tangential Quadrilateral Theorem I, \(\overline{EFGH}\) is tangential.

Glagolev (Elementary Geometry Book I, Planimetry) ended absolute geometry with the following proof, but was rebuked by Fetisov (Proof in Geometry) for omitting L. 2.4. Pogorelov (Geometry, 7^th to 9^th grade) ended absolute geometry with L. 2.3, then began Euclidean geometry with the circumcenter theorem and then the above Pitot Theorem Converse. We have more absolute geometry to do, so we cannot use his organization, but we include his Euclidean proof for students who will teach in a middle school that uses his textbook.

Lemma 2.4
Given \(\overline{EFGH}\) with \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\), F inside \(EI_{EF}\) and G inside \(HI_{GH}\) are not both true.

Proof

\(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\)	Given
\(\overline{EI_{EF}}-\overline{FI_{EF}}+\overline{HI_{GH}}-\overline{GI_{GH}}=\overline{FG}+\overline{EI_{HE}}+\overline{HI_{HE}}\)	Expand sums and differences
\(-\overline{FI_{EF}}-\overline{GI_{GH}}=\overline{FG}\)	Two Tangents Theorem
\(\overline{FG} + \overline{FI_{EF}}+\overline{GI_{GH}}=0\)	is impossible, so F is outside \(\overline{FI_{EF}}\) or G is outside \(\overline{HI_{GH}}\)

Pitot Theorem Converse
If the sums of each pair of opposite sides of a quadrilateral are equal, it is tangential.

Absolute Geometry Proof
Given \(\overline{EFGH}\) with \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\), by the angle bisector theorem, it is possible to construct a circle tangent to \(\overline{EF}\) and \(\overline{FG}\) and \(\overline{GH}\). Suppose that it is not tangent to \(\overline{HE}\). By lemma 2.4, it is possible to draw a tangent from E to K on \(\overleftrightarrow{GH}.\overline{EFGK}\) is tangential. The trichotomy is \(K \equiv H\), K is on \(\overline{GH}\), or K is on the extension of \(\overrightarrow{GH}\). Assume it is on \(\overline{GH}\).

\(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\)	Given
\(\overline{EF}+\overline{GK}=\overline{FG}+\overline{KE}\)	Pitot Theorem using \(\overline{EFGK}\)
\(\overline{GH}-\overline{GK}=\overline{HE}-\overline{KE}\)	Subtract one equation from the other
\(\overline{KH}=\overline{HE}-\overline{KE}\)	Subtract \(\overline{GK}\) from \(\overline{GH}\)
\(\overline{KH}+\overline{KE}=\overline{HE}\)	Add \(\overline{KE}\) to both sides

This contradicts the triangle inequality theorem, so K is not on \(\overline{GH}\). Analogously, K is not on the extension of \(\overrightarrow{GH}\). Thus, \(K\equivH\) and the circle is tangent to \(\overline{HE}\).

Pedal triangle vertices are the feet of perpendiculars dropped on triangle sides or their extension from an arbitrary point called the pedal point. Orange belts will prove the orthocenter theorem, that the altitudes are concurrent at a point called the orthocenter, which makes the orthic triangle a pedal triangle. If the pedal point is the circumcenter, then the pedal triangle is the medial triangle, its sides are mid-segments and its vertices are the midpoints of its parent triangle. Without the parallel postulate, the circumcircle may not exist, but it does for equilateral triangles, so it is a yellow-belt term; medial triangles exist now, but only become important later.

If the pedal point is the incenter, then the incircle touches the triangle at the vertices of the contact triangle, which is pedal. The incircle exists and is unique for every triangle, in contrast to tangential quadrilaterals, which are not fully defined by their sides. We have existence when \(a+c=b+d\), but we never have uniqueness because the length of the diagonal can be any x such that \( 0< x < a+b \). Choose one and then, by SSS, draw in c and d.

Before proving the following theorem, let us state what a quadrilateral is because our definition differs from the rather vacuous definition (four-sided figure) that is given in other textbooks. A quadrilateral is the union of two triangles adjacent on a side. In Geometry–Do, all quadrilaterals are convex; we ignore four-sided concave figures. The definitional diagonal is the adjacent side.

Next, let \(\overline{EFGH}\) be the union of \(\overline{EFH}\) and \(\overline{FGH}\). Let \(P_{E}, P_{F}, P_{H}\) be the pedal triangle vertices of the incenter of \(\overline{EFH}\). Let \(Q_{F}, Q_{G}, Q_{H}\) be the pedal triangle vertices of the incenter of \(\overline{FGH}\). The subscript refers to the opposite vertex; e.g. \(P_{E}\) is on side \(\overline{FH}\) of triangle \(\overline{EFH}\). Calling “Two tangents!” every time we substitute equal segments is tedious, so this will be left tacit.

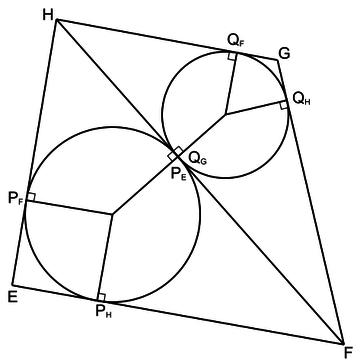
A pedal point is denoted P and, if there is a second one, it is Q; with subscripts, these letters denote the pedal triangle vertices. The incenter, I, is a pedal point; the notation is compatible.

Tangential Quadrilateral Theorem II
The incircles of a quadrilateral’s two triangles are tangent if and only if it is tangential.

Part One
If a quadrilateral is tangential, then the incircles of its two triangles are tangent.

We hope to prove that \(\overline{P_{E}}\) and \(\overline{Q_{G}}\) are the same point; that is, the length of \(\overline{P_{E}Q_{G}}\) is zero. This is a trichotomy with the other two possibilities being \(\overline{FQ_{G}}<\overline{FP_{E}}\) or \(\overline{FP_{E}}<\overline{FQ_{G}}\).

Proof
\(\overline{FP_{E}}=\overline{EF}-\overline{EP_{H}}\) and \(\overline{FQ_{G}}=\overline{FG}-\overline{GQ_{H}}\); thus, \(\overline{P_{E}Q_{G}}=\overline{FP_{E}}-\overline{FQ_{G}}=\overline{EF}-\overline{EP_{H}}-\overline{FG}+\overline{GQ_{H}}\). Here we are assuming \(\overline{FQ_{G}}<\overline{FP_{E}}\). \(\overline{HQ_{G}}=\overline{HG}-\overline{GQ_{F}}\) and \(\overline{HP_{E}}=\overline{HE}-\overline{EP_{F}}\); thus, \(\overline{P_{E}Q_{G}}=\overline{HQ_{G}}-\overline{HP_{E}}=\overline{GH}-\overline{GQ_{F}}-\overline{HE}+\overline{EP_{F}}\). \(2\overline{P_{E}Q_{G}}=\overline{EF}+\overline{GH}-(\overline{FG}-\overline{HE})\) by adding the two equations above. But \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\) by the Pitot Theorem, so \(\overline{FQ_{G}}<\overline{FP_{E}}\) cannot be true. Analogously, \(\overline{FP_{E}}<\overline{FQ_{G}}\) cannot be true, so \(\overline{P_{E}Q_{G}}\).

Part Two
If the incircles of a quadrilateral’s two triangles are tangent, then it is tangential.

Here we assume that \(P_{E}\) and \(Q_{G}\) are the same point, so we will give it one name, T. We hope to prove that \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\) so that we can then invoke the Pitot theorem converse.

Proof
If the incircles of a quadrilateral’s two triangles are tangent, then it is tangential.

\(\overline{EF}+\overline{GH} = \overline{EP_{H}}+\overline{PH_{F}}+\overline{GQ_{F}}+\overline{QF_{H}}\)
            \(= \overline{EP_{F}}+\overline{FT}+\overline{GQ_{H}}+\overline{HT}\)
            \(= \overline{EP_{F}}+\overline{FQ_{H}}+\overline{GQ_{H}}+\overline{HP_{F}} = \overline{HE}+\overline{FG}\)

Tangential Quadrilateral Theorem III
Let \(P_{F}\) and \(P_{H}\) be pedal triangle vertices of \(\overline{EFH}\), \(Q_{G}\) and \(Q_{E}\) be pedal triangle vertices of \(\overline{EFG}\), \(R_{H}\) and \(R_{F}\) be pedal triangle vertices of \(\overline{GHF}\) and \(S_{E}\) and \(S_{G}\) be pedal triangle vertices of \(\overline{GHE}\). Then \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\) if and only if \(\overline{P_{H}Q_{G}}+\overline{R_{F}S_{E}}=\overline{Q_{E}R_{H}}+\overline{S_{G}P_{F}}\).

Expand each addend of \(\overline{EF}+\overline{GH}=\overline{FG}+\overline{HE}\) into the sum of three segments and then reassemble into \(\overline{P_{H}Q_{G}}+\overline{R_{F}S_{E}}=\overline{Q_{E}R_{H}}+\overline{S_{G}P_{F}}\); or vice versa. This is left as an exercise.

Did everybody get the white-belt exit exam question about Saccheri quadrilaterals?

Mid–Segment and Mediator Theorem
The mid-segment of a triangle’s sides is perpendicular to the mediator of its base.

Proof
Given \(\overline{EFG}\), let \(E', F', G'\) be the feet of perpendiculars dropped on \(\overleftrightarrow{M_{GE}M_{FG}}\) from \(E, F, G,\) respectively. By AAS, \(\overline{E'M_{GE}E}\cong\overline{G'M_{GE}G}\) and \(\overline{F'M_{FG}F}\cong\overline{G'M_{FG}G}\); thus, \(\overline{E'E}=\overline{G'G}\) and \(\overline{F'F}=\overline{G'G}\). By transitivity, \(\overline{E'E}=\overline{F'F}\), so \(\overline{E'F'FE}\) is a Saccheri quadrilateral. By the Saccheri Theorem I, \(\overleftrightarrow{M_{E'F'}M_{EF}}\perp\overleftrightarrow{E'F'}\); but, \(\overleftrightarrow{E'F'}\equiv\overleftrightarrow{M_{GE}M_{FG}}\). Thus, the result.

It is an easy corollary of ASA that isosceles triangles have two angle bisectors equal; while not among Euclid’s propositions, it must surely have been known to him. Is the converse also this easy? No. Geometers waited over 2000 years for the converse, which is known as the Steiner-Lehmus theorem. Here is not the classic proof of Jakob Steiner, but a better one because it does not invoke the parallel postulate. It is made possible by Pasch’s Axiom, which was introduced by Moritz Pasch in 1882, about forty years after Lehmus proposed and Steiner solved the problem.

Steiner–Lehmus Theorem
If a triangle has two angle bisectors equal, then it is isosceles.

Modern Proof
Given \(\overline{EFG}\) with the angle bisectors \(\overline{FF*}=\overline{EE*}\), assume that \(\overline{GE}\neq\overline{GF}\). By the greater angle theorem, \(\angle F<\angle E\), and their halves,\(\angle F*FG<\angle E*EG\). By C. 1.5, replicate \(\angle F*FG\) with one ray \(\overrightarrow{EE*}\) and the other inside \(\angle E*EG\); let J be its intersection with \(\overline{GF}\). From \(\angle F*FG<\angle E*EG\) and insideness, \(\angle EFJ<\angle FEJ\). By the greater Side Theorem, \(\overline{EJ}<\overline{FJ}\), so one can lay off \(\overline{FM}=\overline{EJ}\) with M inside \(\overline{FJ}\). By SAS, \(\overline{JEE*}\cong\overline{MFF*}\), which holds the equality \(\angle EJE*=\angle FMF*\). Applying Pasch’s Axiom to the line \(\overleftrightarrow{EJ}\) and the triangle \(\overline{MGF*}\), there exists a point N that is on \(\overleftrightarrow{EJ}\) and between F* and M. In the triangle \(\overline{NJM}\), the interior angle \(\angle NJM\) equals the exterior angle \(\angle NMF\) because \(\angle EJE*=\angle FMF*\). This contradicts the exterior angle theorem and so \(\overline{GE}=\overline{GF}\).

Difficult? It is easier than the classic proof that has auxiliary lines outside the triangle and cites green-belt theorems. It is made possible because we accept “inside” and “between” as intuitive.

For the pedagogic purpose of teaching older students how to teach younger students, and because of its importance to the history of geometry, the classic proof is given at the beginning of the red-belt chapter. This is of interest to students who intend to take a history-of-math class.

Problem 2.11
Given an isosceles right triangle, can you prove that the base angles are each half of a right angle?

No, you cannot prove this! Yellow belts do not have the angle sum theorem (the interior angles of a triangle sum to one straight angle) because its proof cites the parallel postulate. In hyperbolic geometry, the interior angles of a triangle sum to less than a straight angle; \(\alpha + \beta + \gamma < \sigma \);

A rectangle is a quadrilateral with equal angles and a square is a rectangle with equal sides.

Construction 2.4
Inscribe in a circle (1) a square; (2) an equilateral triangle; (3) a regular (equilateral and equiangular) hexagon.

Solution

1. Squares are both rhombi and rectangles, so diagonals are both perpendicular and equal. Draw a diameter and its mediator; they intersect the circle at the vertices.

2. Draw a diameter and a circle of equal radius at one of its endpoints. The other end of the diameter and the intersections of the circles are the vertices.

3. Draw a diameter and circles of equal radius at its endpoints. The ends of the diameter and the intersections of the new circles with the given circle are the vertices.

Are the equal angles in rectangles and in squares necessarily right? No!!! Yellow belts do not have the angle sum theorem; thus, they do not have the quadrilateral angle sum theorem either. By SAS, the four C. 2.4.1 triangles are congruent, so the quadrilateral has equal sides and angles. This is all that we know about the quadrilateral, and all that is needed to prove that it is a square.

Right Rectangle	A rectangle with right angles
Right Square	A right rectangle with equal sides

Yellow belts are responsible for knowing these definitions only so they can contrast what they are doing with what orange belts will be doing after the parallel postulate is introduced. Yellow belts cannot construct either of these figures. When René Descartes invented cartesian coordinates, he did not just construct a grid of squares, he constructed a grid of right squares.

Cartesian coordinates are only useful if the scale is stated so the problem can be applied to some object in the real world. But scaling a geometric figure up or down to represent a real-world object can only be done with the triangle similarity theorem, which states that, if the angles of two triangles are pairwise equal, then then their sides are proportional. But this theorem cannot be proven without the parallel postulate

Suppose I say, “Given a triangle with base \(40.2 cm\) and base angles \(45°\) and \(51°\), what is the length of the median to the base?” This is an easy application of the ASA theorem. You draw the base to the given length, use a protractor to construct the angles and extend their rays to intersect at the apex. You use C. 1.2 to bisect the base and then you use your centimeter ruler to measure from the base midpoint to the apex. It’s \(22.1\) cm!

Now suppose that I try to make this problem realistic by saying, “I have a mortar and wish to shell an enemy anti-aircraft gun. But I cannot measure the distance directly because it is on the other side of an office building and, even if I could get out there with a measuring tape, they would shoot me. So, I send two soldiers \(201 m\) in each direction on my street and have them measure the angle to the enemy gun. They report angles of \(45°\) and \(51°\);. What is the range for my shot?”

Without the parallel postulate, we cannot answer. Just because the base of the triangle on the paper and the triangle in real life have a ratio of one to a thousand is no assurance that the legs or the median to the base are in this ratio. Ballistics is not just different in a hyperbolic world, it does not exist, at least on a large scale. It might be approximately Euclidean on the scale of small arms, but artillery would be pointless because there would be no means of locating the enemy.

Descartes is known as the father of modern philosophy and, as such, he plays a major role in 1st semester college philosophy courses. Even in high school, most students are familiar with his dictum, Cogito, ergo sum; or, I think, therefore I am. Descartes wanted to clear away all tacit assumptions – A noble endeavor, which I share! – and he concluded that “I exist” is the only thing that any of us can really be sure of. From this one axiom, he then set out to prove all knowledge. With all due respect, Descartes failed. His invention of cartesian coordinates tacitly assumes the parallel postulate. Lobachevski was 200 years in his future, though, so we will give him a break.

Common Core tacitly assumes the parallel postulate. We will play a trick on American teachers who skip ahead to the yellow belt exit exam to check that they know this material without reading the chapter. In problems #4, #5 and #6, I define quadrilaterals by their cartesian coordinates, so we are assuming that the world is approximately Euclidean for triangles a few hundred meters across. The American teachers’ insistence on turning easy geometry problems into difficult algebra problems will be hilarious as they futilely throw square roots in every direction.

1. Conway Problem At each vertex, extend the sides of a triangle out by a distance equal to the opposite side. Prove that the six endpoints are concyclic and find the circle center.

2. A triangle has sides of \(13 cm, 14 cm\) and \(15 cm\). What is the inradius?

3. Prove that, if the apex angle bisector and the base mediator do not coincide, then they intersect outside the triangle.

4. Find the circumcenter of a triangle with vertices at \((-3.8, -0.6), (12.7, 0.4)\) and \((1, -27)\).

5. You bought a quadrilateral farm with vertices at \((0, 0), (408, 0), (288, 315)\) and \((68, 285)\) meters. You wish to install center pivot irrigation. Without first drawing the crop circle, how can you be sure that it will touch all four sides? What surveying instrument should you buy to locate the circle center? Where is the center?

6. You own a farm with vertices \((0, 0), (408, 0), (288, 315)\) and \((68, 285)\) meters that uses center pivot irrigation. Subdivide it into two crop circles. Locate the centers so the circles each touch a side and each other with no overlap. How can you be sure that such circles exist? What surveying instrument should you buy? Where are the centers?

7. From a house in the country, construct a dirt road \((30 mph limit)\) to a straight paved road \((50 mph limit)\) to minimize travel time to a nearby town on the paved road.

8. Look up external tangents and then prove this: If two circles touch, then the quadrilateral whose vertices are the tangent points of their external tangents is tangential.

9. Given two sides, an angle opposite one of them and the fact that the angle opposite the other side is acute or that it is obtuse, prove that the triangle is fully defined.

10. Given lines \(\overleftrightarrow{EF}\) and \(\overleftrightarrow{GH}\) with F and H on opposite sides of \(\overleftrightarrow{EG}\), if \(\angle FEG=\angle HGE\), prove that \(\overleftrightarrow{EF}\) and \(\overleftrightarrow{GH}\) do not intersect.

11. Given \(\overline{EFG}\), let \(E', F', G'\) be the feet of perpendiculars dropped on \(\overline{M_{GE}M_{FG}}\) from \(E, F, G\), respectively. Prove that \(\overline{E'F'FE}\) is a Saccheri quadrilateral and that \(\angle E'EF+\angle F'FE\) is the angle sum of \(\overline{EFG}\).

12. Can you construct a line through a point that meets a given line at a given angle?

2.12 Construct a right triangle given

a. a leg and the hypotenuse.
b. the hypotenuse and one acute angle.
c. the sum and the difference of the legs.

2.13 Construct a triangle given

a. the apex altitude and the legs.
b. the base and the two base angles.
c. the base, a base angle and the median to the side of this angle.
d. the base, the median to the base and one leg.
e. the apex angle, its angle bisector and a leg.

2.14 Construct two equal circles whose common chord equals their given radius.

2.15 Construct two equal circles given their common chord and the distance between centers.

2.16 Construct a half equilateral triangle. Other textbooks call this a \(30°–60°–90°\); triangle. Why do we not use their terminology?

2.17 Given \(\overline{EFGH}\) tangential, \(\overline{GH}=\overline{FG}=4\overline{EF}\), how many times can \(\overline{EF}\) be laid off in \(\overline{HE}\)?

2.18 Solve Problem 2.6 if it is known that the angle goes between the centers.

2.19 Let \(\omega1\) and \(\omega2\) be concentric circles with \(\omega1\) inside \(\omega2\) and center O. If E, F are on \(\omega1\) and G, H are on \(\omega2\) and \(\angle OEG=\angle OFH\), prove that \(\overline{OEG}\cong\overline{OFH}\).

2.20 Let \(\overline{EFG}\) be isosceles with \(\overline{EG}=\overline{FG}\) and E' and F' be the feet of the altitudes to \(\overline{FG}\) and \(\overline{GE}\), respectively. Prove that the ray through their intersection bisects \(\angle G\).

2.21 Let \(\overline{EFG}\) be isosceles with \(\overline{EG}=\overline{FG}\) and let P be a point in the interior of \(\overline{EFG}\) such that \(\angle EPG=\angle FPG\). Prove that P is on the median to \(\overline{EF}\).

2.22 Let \(P_{1}, P_{2}, P_{3}, P_{4}, P_{5}\) be distinct points on a circle such that \(\overline{P_{1}P_{2}}=\overline{P_{2}P_{3}}=\overline{P_{3}P_{4}}=\overline{P_{4}P_{5}}\). Prove that \(\overline{P_{1}P_{4}}=\overline{P_{2}P_{5}}\).

2.23 Two chords make equal angles with a diameter through their intersection. Prove that the chords are equal.

Prove the following triangles congruent. Put the triangle vertices in the order that they are proven equal; for instance, “by AAS, \(\overline{EFG}\cong\overline{JKL}\) is shorthand for \( \angle E= \angle J\) and \( \angle F= \angle K\) and \(\overline{FG}=\overline{KL}\). Even if AAS is the correct congruence theorem, if it is a different two pairs of angles or a different pair of sides that are equal, then you will be marked down. Clarity is important!

2.24 Given \(\angle EFG\) with \(\overline{EF}=\overline{GF}\), extend \(\overrightarrow{FE}\) to J and \(\overrightarrow{FG}\) to K such that \(\angle FJG=\angle FKE\). Prove that \(\overline{JFG}\cong\overline{KFE}\).

2.25 Given \(\overline{EF}\) with J and K on the mediator such that \(\overline{EJ}=\overline{FK}\). Prove that \(\overline{EM_{EF}J}\cong\overline{FM_{EF}K}\).

2.26 Given \(\overline{EFG}\) with \(\angle EFG=\angle FEG\), prove that \(\overline{EM_{EF}G}\cong\overline{FM_{EF}G}\).

2.27 Given \(\overline{EF}\) with \(\angle EJM_{EF}=\angle FKM_{EF} and with \(J, M_{EF}, K\) collinear and in that order, prove that \(\overline{EJM_{EF}}\cong\overline{FKM_{EF}}\).

2.28 Given \(\overline{EF}\) and a line through \(M_{EF}\), raise perpendiculars from E and F to intersect the line at J and K, respectively. Prove that \(\overline{EJM_{EF}}\cong\overline{FKM_{EF}}\).

2.29 Given \(\overline{EFGH}\) with \(\angle E=\angle F=\angle ρ\) and \(\overline{EG}=\overline{FH}\), prove that \(\overline{EFGH}\) is a Saccheri quadrilateral.

2.30 Kite is an orange-belt term; look it up. (1) Construct a kite; (2) Without the Pitot theorem converse., prove that kites are tangential; (3) Prove that one diagonal mediates the other.

2.31 The perpendicular length theorem has one corollary, but some books also say, if a line is perpendicular to one of two parallels, it is perpendicular to the other too. Why don’t we? Is it also a corollary that tangents to a circle at the endpoints of a diameter never meet?

2.32 Johnny Geometer has his own proof of the isosceles triangle theorem! Sound? Or not? Given \(\overline{EFG}\) with \(\overline{GE}\) and \(\overline{GF}\) equal, by SSS, \(\overline{EFG}\cong\overline{FEG}\) and thus \(\angle EFG=\angle FEG\).

2.33 Suppose you teach middle school and they omit ASA. Can you prove the isosceles triangle theorem converse with AAS? If they omit AAS, can you prove just this special case of it?
Given the hypotenuse and one angle of a right triangle, it is fully defined.

2.34 Let \(E, F, G\) be on an \(O-circle\) such that \(\overline{EF}<\overline{FG}\). Prove that \(\angle OM_{EF}M_{FG}<\angle OM_{FG}M_{EF}\).

Suppose you are building an \(8'\times12'\) cabin that will rely entirely on solar power. The roof should be asymmetric, with the southern face of a mild pitch to support the solar panels while the northern face is more steeply pitched. Also, for a short \(8'\) span, asymmetric trusses are stronger.

The strong roof truss. For an asymmetrical roof, we will modify the Fink truss so the attic is a half equilateral triangle. Bisect the ceiling joist and construct an equilateral triangle on the northern side. The rafters rest on the southern wall and on the triangle apex. A beam from the foot of the triangle meets the rafter at a right angle.

The hollow roof truss. The ceiling joist and the rafters are the same, but the support beams are removed to house a round water tank. Water tanks can be quite heavy so, even if there were not a need for a large southern roof face, it is a good idea to build an asymmetric roof so the water tank is near a wall to help support it. Have a hot- and a cold-water tank on either end of the cabin and put strong roof trusses between them so the roof does not sag in the middle.

By the Incenter Theorem, the angle bisectors intersect at the center of the incircle. Drop a perpendicular to the ceiling joist and extend it to the other side of the circle so it is a diameter. Measure it with a ruler to determine how large of a tank you can have. Orange belts will learn of the right triangle incircle theorem, that the indiameter is the sum of the legs minus the hypotenuse. Because our roof’s apex angle is right, this equation would give the same answer.

If you are off the grid because of a war, dig into the reverse slope (away from the enemy) and build your cabin with the steeply pitched roof facing uphill with gun ports so you can fire on the enemy should they crest the hill. Use the strong roof truss every \(16''\) throughout and with double-thick plywood. Pile dirt and rocks onto the roof to protect it from mortar shells. If a tank crests the hill, run. They cannot depress their gun to shoot downhill, but they can drive over you.

Orange Belt Geometry for Construction Workers , next, originally came at the end of the orange-belt chapter, which is logical, because the approximations to the Tudor arch do not exist in non-Euclidean geometry. However, few construction workers survive orange belt, so I moved this section forward. Purists can restrict themselves to the classic arches and bridges, while those who must approximate can pretend that they are orange belts and have the parallel postulate. The Tudor builders were working from scratch, but arches today are almost always a façade on an existing structure, so approximations are essential to the modern construction company. Right rectangles do not exist in hyperbolic geometry, so only orange belts can give width to boards. This section will draw plans for Fink and asymmetrical trusses using \(2''\times 6''\) boards.

The single best piece of advice that I can offer construction workers is to use the metric system. (I have seen plumbers almost come to blows because they messed up the laying of sewer pipe at \(1''\) drop every \(8'\). A drop of one centimeter every meter – a \(1%\) downgrade – is the same thing, but it is a lot easier.) I would have scaled these roof truss figures at \(1 cm = 1 foot\), but they would not fit in the book. Construction 3.3 draws a line parallel to a given line through a point not on the line, but you can do this now with a rolling ruler or by sliding a plastic triangle along a straight edge. I encourage you to draw these roof trusses at \(1 cm = 1 foot\) now, before next semester.

Arches and bridges are the classic application of geometry to the construction trades.

Suppose that, while a house is being built, the workers must cross a ditch that is bridged with a \(2” X 12” X 12’\) board. It is bouncy underfoot and dangerously close to breaking when a fat man with a wheelbarrow full of sand is at its center. Inscribe an arc in the board from one corner to the center point of the other side and across to the other corner. Cut along the arc, steam bend another board over it and attach the two boards with corner braces. The radius of an arc inscribed in a \(2” X 12” X 12’\) board is \(19’ 3”\) because after being planed, It is \(1.5”” X 11.5”” X 12”’\). An arc described in a \((w X h)\) rectangle has radius \(r = \frac{4h^{2}+w^{2}}{8h}\) because, by Pythagoras \((r-h)^{2}+(\frac{w}{2})^{2} = (r)^{2}\).

To inscribe an arc in a rectangle, find the center using the circumcenter theorem with your three points being two corners on the same side and the midpoint of the opposite side. For aesthetic reasons, it is important that the several arcs in your design all have the same radius. So, if one arc is given, choose any three widely spaced points on it and apply the circumcenter theorem.

Arches with one center like this are called Roman and their chord is called the spring line. A Gothic arch has two centers; if they are at the endpoints of the spring line, it is called equilateral. If the centers are on the extensions of the spring line, it is called lancet; if inside, it is called deep.

If you know the height and width, then draw mediators of the legs of the triangle defined by the end points of the spring line and the height of the arc above its midpoint. Where the mediators intersect the spring line or its extension are the two arc centers. If they intersect the spring line before they intersect each other, the centers must be below the spring line equally distant past where the mediators intersect each other. How far past is indeterminate. This is called a pointed Roman arch because it does not look very Gothic.

The Goths were a long time ago and use of their arches gives a building a medieval look. The ogee arch is Gothic. It is very pointed, which is inefficient as a window, but symbolic in a church. The onion dome is like the ogee arch, but you should not use it unless you are Eastern Orthodox.

Ogee Arch Circumscribe a rectangle around an equilateral triangle. Draw arcs centered at the midpoint of the base and the two upper corners with a radius of half the base.

In America, a Roman arch is often seen above a window, door or gate, probably because it is the simplest arch and the only one familiar to most construction companies. It is squat, which is fine if it is on top of a rectangle but, if it is the entire opening, then its corners are too sharp. A Tudor arch is also squat, but it has upright corners and works well for wide entrances to big buildings.

Tudor Arch Quadrisect the spring line, \(\overline{EF}\), so \(Q_{1}\) is the midpoint of \(\overline{EM_{EF}}\) and \(Q_{2}\) is the midpoint of \(\overline{M_{EF}F}\). Construct an equilateral triangle \(\overline{Q_{1}JQ_{2}}\) with J below the spring line and extend \(\overrightarrow{Q_{1}J}\) to K so \(\overline{JK}=\overline{Q_{1}J}\) and \(\overrightarrow{Q_{2}J}\) to L so \(\overline{JL}=\overline{Q_{2}J}\). Draw arcs (called haunch arcs) centered at \(Q_{1}\) and \(Q_{2}\) with radii \(\overline{Q_{1}E}\) and \(\overline{Q_{2}F}\) to intersect \(\overline{JQ_{1}}\) at M and \(\overline{JQ_{2}}\) at N, respectively. Draw arcs (called crown arcs) centered at K and L with radii \(\overline{KM}\) and \(\overline{LN}\) to intersect at the apex. The height of the apex of the Tudor arch is \(\frac{\sqrt{6}-\sqrt{3}}{2}\approx35.87%\) of its width, the length of the spring line.

Suppose that a beam bridge made of reinforced concrete spans a canal four meters wide and it is \(h\) meters above the concrete sides of the canal. This is ugly, so the city has hired you, a mason, to construct a façade to make it appear that the bridge is a Tudor arch made entirely of brick.

There are many possible arches with four centers but, if we are going to call ours Tudor, then it must coincide with the classic one when given a height \(\frac{\sqrt{6}-\sqrt{3}}{2}\) of the width. Also, we must quadrisect the spring line regardless of the height. If the centers of the haunch arcs are near the edges of the spring line, the arch would look Gothic but with rounded corners. If the centers of the haunch arcs are near the midpoint of the spring line, the arch would look like a pointed Roman. But putting the centers of the haunch arcs on the quartile points makes it look Tudor.

Construction 2.2
Construct a Tudor arch given a height and width approximately that of the classic Tudor arch.

Solution
Quadrisect the spring line, \(\overline{EF}\), so Q is the midpoint of \(\overline{M_{EF}F}\). Raise a perpendicular to \(\overleftrightarrow{EF}\) from \(M_{EF}\) and lay off \(\overline{M_{EF}F}\) to be the given height. From F, raise a perpendicular to \(\overleftrightarrow{EF}\) on the same side as K and lay off \(\overline{KL}=\overline{FQ}\). Connect \(\overline{KJ}\). From K, raise a perpendicular to \(\overleftrightarrow{KJ}\) on the same side as \(M_{EF}\) and lay off \(\overline{KL}=\overline{FQ}\). Connect \(\overline{QL}\). Where its mediator intersects \(\overrightarrow{KL}\) is the center of the crown arc, O, and its radius is \(\overline{OK}\). The haunch arc is centered at Q and has radius \(\overline{FQ}\); the arcs meet on \(\overrightarrow{OQ}\). Analogously on the other side.

Proof that this coincides with the Tudor arch when given a height \(\frac{\sqrt{6}-\sqrt{3}}{2}\) of the width comes later.

Suppose that the Tudor arch we just designed was not a façade but was meant to support the roadbed. Would it work? No. Brick is not as strong as stone and – far more fatal to the design – the mortar between them is much weaker than the bricks. Since all the bricks are rectangular, they can only describe an arc if there is mortar between them and it is in a wedge shape. Brick arches look elegant and are recommended for aesthetic reasons, but they are not weight bearing.

The Romans cut stones into isosceles triangle frustums (isosceles triangles cut by lines parallel to their bases) for bridge construction. This works in areas free of earthquakes but, because gravity presses them together, if the bridge is jolted, it all comes crashing down. In modern times, bolting the stones together would make it earthquake resistant, but a more fundamental flaw is that it is only strong if it is most of a semicircle, which is too steep for vehicles. Flatter Roman arches are weak in the center and they push outwards as well as down, so they must have sturdy foundations. Also, if the river rises, flood water pushes on the sides of the bridge near the banks and, if the river is flowing fast, it can push the stones out of place and cause a collapse.

Engineers wish for an arch flat enough for vehicles to climb over but with upright corners so the weight presses straight down and the roadbed is above high waters. An ellipse would work, but this is not feasible because every stone would be unique and it is not practical to readjust the saw for each cut. However, if you have two saws, they can be calibrated to cut the triangle frustum needed for arcs of two different radii. Thus, the Tudors approximated an ellipse with haunch arcs of one radius and a single crown arc that goes all the way across rather than meeting in a pointed apex. With modern construction, Tudor bridges are strong enough for truck traffic.

Tudor Bridge Quadrisect the spring line, \(\overline{EF}\), so \(Q_{1}\) is the midpoint of \(\overline{EM_{EF}}\) and \(Q_{2}\) is the midpoint of \(\overline{M_{EF}F}\). Construct an equilateral triangle \(\overline{Q_{1}JQ_{2}}\) with J below the spring line. Draw arcs (called haunch arcs) centered at \(Q_{1}\) and \(Q_{2}\) with radii \(\overline{Q_{1}E}\) and \(\overrightarrow{Q_{2}F}\) to intersect \(\overrightarrow{JQ_{1}}\) at M and \(\overrightarrow{JQ_{2}}\) at N, respectively. Draw an arc (called the crown arc) centered at J with radius \(\overline{JM}=\overline{JN}\).

The Tudor bridge is just like the Tudor arch except, instead of extending the legs of the equilateral triangle an equal distance to find the two centers of the crown arcs, we take the apex of the equilateral triangle to be the center of the single crown arc. An isosceles triangle taller/shorter than an equilateral triangle makes the bridge flatter/steeper, but this is not recommended. The height of the classic Tudor bridge is \(\frac{3-\sqrt{3}}{4}\approx31.70%\) of its width, the length of the spring line.

Is this design useful to carpenters? No. Archimedes, a Syracuse mathematician who studied in Alexandria shortly after the time of Euclid, invented what is now called the Archimedes’ trammel. It draws ellipses or, if a router is attached to the arm, cuts them. Proof that this works is beyond the scope of this book, but it does, so carpenters have no need for approximating an ellipse with arcs. Note that the word trammel, without the adjective, refers to a board with two awls clamped to it. Pushing one into wood and rotating the board allows the other to scratch an arc, so the device functions just like a geometer’s compass, but it can reach across a sheet of plywood.

Geometers drawing poster-size figures can buy a pencil trammel at a shop for wood workers. It is time consuming to adjust, but it draws circles larger than the 54 cm of the Alvin 702V.

Construction 2.5 requires that the height and width are approximately that of the classic Tudor arch; that is, in the range \( \frac{1}{4}w < h < \frac{\sqrt{2}}{2}w \). To draw an arch to an arbitrary height requires that the radius of the haunch arc be a function of height; specifically, \(\frac{2h}{3}\). This is called generic because squat/tall generic arches look like Roman/Gothic arches with rounded corners and, for the same height as the classic Tudor arch, the generic arch looks Tudorish but it is not exactly the same.

wo thirds of \(\frac{\sqrt{6}-\sqrt{3}}{2}\) is \(\frac{\sqrt{6}-\sqrt{3}}{2}\approx35.87%≠25%\) of the width, so it is not mathematically Tudor.

We will cite C. 3.11; construction workers must skip ahead and just take it as a cook-book recipe.

Generic Arc Bisect the spring line, \(\overline{EF}\), and raise a perpendicular from \(M_{EF}\) to K so that \(\overline{M_{EF}F}\) is the given height. By C. 3.11, trisect \(\overline{M_{EF}F}\) and call two-thirds the height x. Locate \(Q_{1}\) and \(Q_{2}\) on the spring line so \(\overline{EQ_{1}}\) and \(\overline{Q_{2}F}\) are x long. From F, raise a perpendicular to \(\overleftrightarrow{EF}\) on the same side as K and lay off \(\overline{FJ}=\overline{FQ_{2}}\). Connect \(\overline{KJ}\). From K, raise a perpendicular to \(\overleftrightarrow{KJ}\) on the same side as \(M_{EF}\) and lay off \(\overline{KL}=\overline{FQ_{2}}\). Connect \(\overline{Q_{2}L}\). Where its mediator intersects \(\overline{KL}\) is the center of the crown arc, O, and its radius is \(\overline{OK}\). The haunch arc is centered at \(Q_{2}\) and has radius \(\overline{FQ_{2}}\); the arcs meet on \(\overrightarrow{OQ_{2}}\). Analogously on the other side.

Tudor Arc	Generic Arc

Problem 2.35
Prove that, for any \(x < h \), the generic arch’s haunch and crown arcs are tangent.

Problem 2.36
A sewer pipe at a \(1%\) downgrade is \(1 m\) above the city line, which is \(5 m\) away. You will use two \(22.5°\) elbows and then enter the city line at a \(1%\) downgrade. If pipe is cut \(3 cm\) from the bend in the elbow, how long is the hypotenuse pipe? Then, how far to the city line?

When I was in high school (1984) I entered the Balsa Bridge Building Contest with a truss design. The roadbed twisted and the trusses turned into an S-shape when viewed from the top; it did not break, but it very quickly deformed enough to fail. The side view showed triangles galore, but the downward view showed no triangles, just some cross braces between the trusses. My sad balsa wood bridge should serve as a cautionary tale about seeing things in only two dimensions.

How many students were rolling their eyes when they got to Problem 2.7 about Poe’s pendulum? You should have been. Generations of students have read The Pit and the Pendulum in their American Literature class with nary a dissenting voice. When restricted to the plane, our solution to Problem 2.7 is sound; but is that big blade really restricted to the plane? Monkish ingenuity notwithstanding, when the blade is going fast near the nadir of its swing, if it is out of line with its motion, the air will push the leading edge even more out of line. The trailing edge does not act as a fin because air that hits the leading edge slides down the length of the blade and prevents still air from pushing the trailing edge back into line. That big blade will start spinning on its cable and will eventually be doing a languid circle around the man strapped to the floor, who is probably by then loudly mocking his executioners for their weak engineering skills.

Another unquestioningly accepted theory is IS-LM Analysis. This is two equations, the income identity and the demand for real money holdings, in two variables, national income and the interest rate. When students point out that the obvious policy prescription is to print money to hold the interest rate at zero, economists talk about how these curves “shift” in response to inflation. Bad move! Curves do not shift. What is actually happening is that there are three equations in three unknowns and economists initially tried to assume away the third dimension by declaring the price level to be constant. When that did not work, they turned their problem into a sequence of problems, each with a constant price level but, in some hazily defined way, shifted from the previous problem. Their near-religious devotion to “data” blinds them to the fact that IS-LM Analysis is based on deductive logic, not statistics, and that it is missing an axiom.

My Axiomatic Theory of Economics has its own axiom set, distinct from the two-going-on-three axioms of John Hicks’ IS-LM Analysis. But the point is, if your problem is three dimensional, then model it with three equations and then simultaneously solve them for all three variables. If this seems daunting, then learn the needed math. Looking at a two-dimensional slice of a three-dimensional problem because the graphs are easy to draw and/or because you only know how to solve two equations in two unknowns does not result in a simplification; it results in nonsense.

Adjacent	The perpendicular from a triangle vertex to the opposite side’s extension
Altitude	The perpendicular from a triangle vertex to the opposite side’s extension
Angle11	Two rays, called the sides, sharing a common endpoint, called the vertex
	\(\angle F\) if there is one angle at F or \(\angle EFG\) for the angle between \(\overleftrightarrow{FE}\), \(\overleftrightarrow{FG}\) Acute An angle that is less than a right angle Apex The angle opposite the base of a triangle Base In a triangle with a base, the angles at either end Complementary Two angles that sum to one right angle Exterior The angle supplementary to an interior angle Interior An angle inside a triangle or quadrilateral at a vertex Obtuse An angle that is greater than a right angle Right The bisection of a straight angle Straight An angle formed by a line with its vertex being a point on that line Supplementary Two angles that sum to one straight angle Vertical Angles across from each other at an intersection
Arc	Part of a circle; within equal circles, angles at the center and the arcs they cut off are a transformation of each other.
Area12	The number of squares(geometry means “Earth measure” so, initially, individual wheat plants) that fill a triangle or union of triangles; A=|\(\overline{EFG}\)|
Auxiliary	Lines or arcs not given whose intersection goes beyond analytic
Axiom	A proposition that is assumed without proof for the sake of studying the consequences that follow from it
Base	The side of an isosceles triangle bracketed by the equal angles; b or B The side of a triangle opposite the apex angle or the one that it is built on, or the side of a quadrilateral called the base for reference purposes.
Bi–Conditional	A statement of the form p if and only if q. It is true if both p and q are true or both p and q are false. p implies q; also, q implies p. Proof of neither implication can cite the other implication. If and only if is abbreviated iff.
Bisect	To divide a segment or an angle into two equal parts, called halves
Center Line	The mediator of the base of an isosceles triangle
Chord	The segment between two points on a circle
Common	The segment between the intersection points of two circles
Circle	All the points equidistant from a point, which is called the center
Circum	Circle A circle that intersects a figure at its vertices Center The center of the circumcircle
Collinear	A set of points that are all on the same line
Concentric	Two or more circles with the same center but different radii
Congruent	Two triangles whose areas and whose sides and interior angles are equal; congruence theorems prove that only three are needed to prove the rest.
Contradiction, Proof by	To prove that statement X implies statement Y, assume that X is true and Y is not true and show that this is impossible.
Contrapositive	To prove that statement p implies statement q, assume that p is true and q is not true and show that this is impossible.
Converse	Given the statement that X implies Y, the statement that Y implies X
Convex	The segment between two points interior to two sides is inside the figure
Diagonal	Segments connecting non-consecutive quadrilateral vertices; p and q Definitional The adjacent side of the two triangles in a quadrilateral
Diameter	A chord that crosses the center of a circle; d or D
Dichotomy	Proof by contradiction when there are two possibilities
Endpoint	A point at the end of a segment, arc or ray
Equal	Comparable magnitudes that are not less than nor greater than each other
Equidistant	Two pairs of points that define two segments of equal length
Equivalence class	A set of objects that are equal, congruent, similar or parallel
Relation	A set and a transitive, reflexive and symmetric relation
Equivalent	Conditions, any two of which are bi-conditional
Extend	Construct the line fully defined by a segment; produce is an archaic term
Figure	A set of points. They may be alone or joined in lines, segments and arcs.
Foot	The intersection when one drops a perpendicular from a point to a line
Fully Defined	A figure with the given characteristics is unique, if it exists
Hypotenuse	The side of a right triangle opposite the right angle; \(w\)
In	Circle A circle that touches each side of a figure Center The center of the incircle diameter The diameter of the incircle; d
Isometric	A transformation that preserves lengths; by SSS it also preserves angles
Length	The unique measure of how long a segment is; |\(\overline{EF}\)|
Legs	The sides of a triangle other than the base or the hypotenuse
Lemma	A theorem used for proving other more important theorems
Line	A segment extended in both directions; denoted \(\overleftrightarrow{EF}\) if \(\overline{EF}\) is the segment
Line of Centers	The line that passes through the centers of two circles
Locus	All the points that satisfy a condition; the plural is loci (lō-sī)
Magnitude	A set with both an equivalence relation, = , and a total ordering, \(\leq\)
Median	A segment from a vertex of a triangle to the midpoint of the opposite side
Mediator	The perpendicular bisector of a segment.
Midpoint	The point where a segment is bisected
Mirror Property	Reflections preserve distance; see the mirror problem and P. 2.3
Mid–Segment	Triangle A segment connecting the midpoints of two sides
Non-Euclidean	A postulate set that contains one that contradicts the parallel postulate
Ordering	TA set and a relation, \(\leq\), that is transitive, reflexive and anti-symmetric Total           \(a \leq b\) or \(b \leq a\) for every a,b in the set
Pedal Point	A point from which perpendiculars are dropped onto the sides or the extensions of the sides of either a triangle or a quadrilateral
Perpendicular	A line whose intersection with another line makes a right angle
Postulate	The axioms that are specific to geometry, not to other branches of math
Quadrilateral	The union of two triangles adjacent on a side such that it is convex; \(\overline{EFGH}\) Rectangle A quadrilateral with equal angles Rhombus A quadrilateral with all equal sides; plural, rhombi Right Rectangle A rectangle with right angles Right Square A right rectangle with equal sides Saccheri A quadrilateral with two opposite sides equal and perpendicular to the base Square A quadrilateral with two opposite sides equal and perpendicular to the base Tangential A quadrilateral for which an incircle exists
Radius	A segment from the center of a circle to the circle; plural, radii
Ray	A segment extended in one direction; denoted \(\overrightarrow{EF}\) if \(\overline{EF}\) is the segment
Reflexive Relation	A relationship that is always true of something when compared to itself
Relation	A true/false operator on an ordered pair of elements from a given set
Segment	All the points along the shortest path between two points; \(\overline{EF}\)
Side	Sum Half the sum of two lengths or of two angles Triangle One of the three segments that form a triangle Quadrilateral An uncommon segment of one of its triangles
Symmetric Relation	A relation that can be stated of two things in either order
Tangent	A line that touches a circle at exactly one point; if its length is referred to, this means the segment between the two points that define it.
Theorem	A statement requiring proof using postulates or already proven theorems
Touch	To intersect at exactly one point, neither less often nor more often Touching Point          the tangent point; also called the point of tangency
Transitive Relation	If a relation is true for a and b and for b and c, then it is true for a and c
Triangle	The segments connecting three points such that the figure is convex; \(\overline{EFG}\) Contact The pedal triangle if the incenter is the pedal point Egyptian A triangle with sides 3, 4 and 5 units long Equilateral A triangle with all sides equal Half Equilateral An equilateral triangle cut at its center line Isosceles A triangle with two sides equal Obtuse A triangle with one angle obtuse Pedal Drop perpendiculars from the pedal point; connect Right A triangle with one angle right
Trichotomy	Proof by contradiction when there are three possibilities
Undefined Terms	Concepts that even small children have an intuitive understanding of; between, inside, plane, point, shortest path and straight
Under Defined	Not enough given information; the solutions are infinite in number
Vertex	The intersection of two lines, rays, or sides of a triangle or quadrilateral