In my 1999 Simplified Exposition of Axiomatic Economics, I write:

Supply and demand curves are different depending on the time unit chosen. Mainstream economists provide no proof that their predicted prices are independent of their choice of time unit. For example, will thirteen predicted weekly quantities be the same as three predicted monthly quantities?

A large part of the problem with supply and demand is that it is used descriptively, but called predictive. It is easy to predict the past. Economists just observe the quantity produced one month and what it sold for and they put a little × over that spot. Then, by pure conjecture, they draw four tails on their × to fill their graph paper. Supply and demand has never been used predictively, not even to make bad predictions. × marks the spot is a purely descriptive technique. Since they are using the 20-20 vision of hindsight, they can do this for three months in a row and, to nobody’s surprise, the sum of the quantities is the quarterly quantity. In the real world, price is constant for years at a time but, for most companies, their weekly and monthly sales figures swing wildly and unpredictably, sometimes by several fold from one month to the next.

My $1000 challenge:

I will pay $1000 to any economist who can provide a formal mathematical proof that supply and demand curves intersect in exactly the same place regardless of whether the time unit is a day, a week, a month or whatever. Do not forget to mention elasticity, which is well-known to be a function of this time unit. To receive the $1000, your proof must be published in a refereed journal. The idea is not to convince me, who has spurned supply and demand and went my own way, but to convince a journal editor so that I may take your arguments as representative of Neoclassical Economics.

Click here for proof that I pay the prizes I offer.

The time unit is important because the differentials do not converge to the derivative. Economists use calculus freely, slavishly imitating physicists as though supply were just like velocity, but they do not have convergence. Doing calculus without convergence is like driving a car without a transmission.

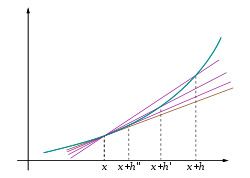
For example, if the vertical axis is distance and the horizontal axis is time, then the graph above could represent the position of a golf ball and the slope of the tangent line its velocity. Where the graph is steep, the ball is quickly changing its position, that is, it has a high velocity.

If one wished to measure the ball's current velocity, one could take a picture of it now and then take another picture ten seconds later. The difference in position divided by ten is a measure of the ball's velocity. But it is a coarse measure of the ball's current velocity, as a lot may change before the second picture is taken.

A better measure of the ball's current velocity is to take a picture of it now and then take another picture one second later. Better yet, a video camera could be used which takes pictures every 30th of a second. With flash photography we can obtain quite fine accuracy, as with the photo below, but there is always some time delay before the second picture is taken. There is no “velocity meter” that gives us the current (instantaneous) velocity the way a camera gives us the current position.

How do we know where the ball was between photos? Intuition tells us that the ball was in points of space between where it was seen, but it may have darted off on a side journey, disappeared entirely or perhaps appeared momentarily on the dark side of the moon before re-joining our intrepid photographer.

We just do not know where the ball was between photographs. It is an axiom of physics that energy and momentum are both conserved. It is not a result. Darting off on side journeys would violate these Conservation Principles.  Physicists are not prepared to forsake these long-held axioms because someone raises impertinent questions about where a golf ball was between photos. Brushing impertinent questions aside is the whole point of having axioms. If physics were not based on the axiomatic method, it would degenerate into a skittish empirical science like Post-Autistic Economics, where everybody has an opinion, just like everybody has an _______.

Supply is the economic version of velocity and economists do not have a “supply meter” any more than physicists have a “velocity meter.”

If one wished to measure a factory's current (instantaneous) output, one could take a count of their inventory now and then take another a year later and add sales to learn how many widgets they are supplying. But it is a coarse measure of the factory's current output, as a lot may change before the second count is taken. It is well-known that time is the most important determinant of elasticity. In a year's time, people can adapt: workers can be re-trained, special-order machinery can be commissioned, crops can be planted, etc.. Clearly, a year is too long for the time unit of supply. A better measure of the factory's current output is to take a count of the inventory now and then take another a month later. Better yet, one might do this every week, every day or even every hour.

But are these measures of supply really “better” in any sense? They do not converge. The hourly figures would be all over the chart depending on whether the experiment was conducted in the daytime or at night, while the machines were running smoothly or wracked by malfunctions, etc.. Prices exist at every instant, so let us take our instant to be 3:00 a.m. on Sunday morning. A price for widgets exists at this moment, for one can certainly go online and order one. But if economists had established an hour to be their time unit, when they go to construct their supply and demand curves, they would find that supply everywhere is zero. There are no factories running.

In my Simplified Exposition of Axiomatic Economics, I write:

Even if a factory is temporarily closed for a week or a month, the price of its product is hardly affected because the total amount of phenomena in existence is hardly affected. Yet during that week or month the supply is zero. Mainstream economics, which relates price to supply, is unable to explain why the price does not increase dramatically as inspection of the supply and demand curves predicts that it should.

So what should the time unit be? A week? A month? It has got to be one or the other and they produce different results. And the different results obtained by different time units do not converge to anything.  There is no axiom in Neoclassical Economics equivalent to the Conservation Principles of physics that assures convergence.

In my Simplified Exposition of Axiomatic Economics, I justify my decision to abandon supply and demand in favor of my own axioms in a number of ways, but none more important than this one:

The method of mainstream economics really has a third variable which is never mentioned and that is the time unit for supply and demand. It is well known that elasticity is a function of this time unit and, if this is true, one calculates a different price depending on whether one speaks of weekly or monthly supply and demand. This is an inconsistency since there can only be one price and it is not dependent on the caprice of an economist when he decides how often to conduct his surveys. This is a point that is glossed over in mainstream texts. A detailed discussion of the time unit chosen for supply and demand is never given and many texts neglect to mention the need for choosing one at all. Yet in their chapter on elasticity, every textbook lists time as a factor, sometimes as the most important factor.

Clearly, there can only be one price and it is not dependent on the caprice of an economist when he decides how often to conduct his surveys any more than the velocity of a golf ball is dependent on how many frames per second the video camera I have purchased operates at. If my camera operates at 30 frames per second and yours at 24 frames per second and we stand side-by-side filming a golf ball sailing past us, we should report close to the same velocity. All of Neoclassical Economics will fall like the House of Usher if it is seen that the prices and quantities it predicts depend entirely on a parameter plucked out of thin air and not on actual market forces.