The Black-Scholes model of the market for an equity makes the following explicit assumptions:

• It is possible to borrow and lend cash at a known constant risk-free interest rate.
• The price follows a geometric Brownian motion with constant drift and volatility.

Also, Black and Scholes make the simplifying assumptions that all securities are perfectly divisible, there are no transaction costs or dividends and there are no restrictions on short selling.  These are just simplifications that later, more complicated versions, have worked around.  So there are really only two essential assumptions made by quantitative analysts - quants.

Let us begin by considering Black and Scholes’ first axiom.  A forum discussant, Suzy, writes:

I am an economist by training and spent 25 years in the banking industry.  I have personally sat in loan committee meetings and had bank examiners demand that we “not discriminate against low and moderate income borrowers.”  Never mind that the reason they are low and moderate income in the first place is their inability to make good financial decisions...  like establishing a steady work history, paying bills on time, living within their means, obeying the law, buying insurance to guard against catastrophic illness or property loss, (women) having multiple children with multiple men.  And on, and on.

The CRA was well intentioned, and lawmakers from both sides of the aisle rightly noted the positive effects that homeownership can have on a society.  The problem was, these middle and upper class lawmakers made the erroneous assumption that if you put poor people in houses, they would suddenly start behaving like financially responsible middle class people.  All of a sudden lawnmowers would replace lottery tickets and backyard barbeques would take the place of drive by shootings.  Alas, these hopes for change were empty promises as they always are, and borrowers who had to get their down payments from “third party non-profit agencies” (by the way, someone always makes a profit, otherwise why are they in it) had nothing to fall back on when the hot water heater broke or the roof leaked.  The houses fell into disrepair and by the time the foreclosure papers were posted, the occupants and hopes of any recovery by the lender long gone.  But the originating lender didn't care...  the loan had been sold, not their problem any more!

There is more blame to go around...  mortgage companies and builders soon realized there was money being printed and there sprung up companies that specialized in getting subprime borrowers into low cost (and low quality) housing.  You probably heard them advertising on the radio and saw the ads in the Sunday paper.  Did you ever wonder what kind of people would need a no-doc loan?  And who would be stupid enough to make such a loan?  I think we all know the answer to that now...  the ultimate lender was of course Fannie Mae or Freddie Mac, the original loan having long since been sold by the originating bank.  All that bad paper, and Franklin Raines out the back door with his suitcase full of money...

Here, Suzy is referring to the Community Reinvestment Act (CRA) that was passed in 1977, four years after Black and Scholes introduced their groundbreaking axiomatic system.  In 1994 the Policy Statement on Discrimination in Lending set severe penalties for banks that refused to steer loans to people based on their ethnicity.  From 1994 until the housing market collapsed a decade later, banks were not allowed to operate as businesses but rather were required to implement an experiment in social engineering.

Clearly, the Community Reinvestment Act and the Policy Statement on Discrimination in Lending flies in the face of Black and Scholes’ first axiom by systematically discriminating against segments of the population in the distribution of credit.  Contra Black and Scholes, it is NOT possible to borrow and lend cash at a known constant risk-free interest rate.  Instead, loans are made on the basis of ethnicity and other non-economic factors, in spite of their known risks.

In reality, the distribution of credit has nothing to do with risk and everything to do with the government steering money to favored races and favored activities.  For instance, a sedan with a trunk ornament that looks like it was stolen off the Red Baron’s Fokker tri-plane costs about as much as a Bridgeport milling machine.   But banks will loan money to buy the former, not the latter.  Some activities, like putting minorities in McMansions, are favored and others, like starting small businesses, are just not. ^[Note]

In spite of the fact that one can hardly walk three blocks in Los Angeles without encountering a Korean-owned grocery store, Korean banks have in the past and continue to loan just about any of their citizens $10,000 to start a grocery store in America.  Vietnamese banks will loan just about any of their citizens $10,000 to start a nail salon in America.  How many American grocers, beauticians or machinists are being given a similar start in businesses here?  None.   But, if you have worked the checkout counter in a Korean-owned grocery for six months, you will have no difficulty finding a bank that will help you drive back and forth to your job in a four-wheel-drive pickup with 36” rims and a little ladder up to the cab.  You’re a big man now!  Your congressman would be proud of you.  Consumption accounts for two-thirds of GNP, you know.

In my 2004 Critique of Austrian Economics, I quote at length a passage from my 1999 book:

I assert that, during boom times, capital is being wasted by every company, from the largest multinational down to the smallest mom-and-pop outfit…

Thus, boom times are characterized by a transfer of capital from smaller companies to larger ones, and the big ones waste it.  Also, while small businesses cannot get credit during a boom, home loans and car loans are easy to obtain, so a lot of capital is converted directly into consumer goods (1999, p. 160-161).

I argue that the failure of Black and Scholes to anticipate that the CRA would up-end their first axiom is the principle cause of our current financial crisis.  Who among you would deny this?

Contra Milton Friedman, assumptions DO matter!

Instead of Black-Scholes, I recommend the following axiomatic system.  Notice that this system does NOT make any ridiculous assumptions about credit being distributed in a fair and even-handed manner.  Also, notice that my third axiom is compatible with Black and Scholes' second axiom, that price follows a geometric Brownian motion with constant drift and volatility.  I have no argument with Black and Scholes’ second axiom.

1)	One's value scale is totally (linearly) ordered:
	i)	Transitive;	p q and q r imply p r
	ii)	Reflexive;	p p
	iii)	Anti-Symmetric;	p q and q p imply p = q
	iv)	Total;	p q or q p
2)	Marginal (diminishing) utility, u(s), is such that:
	i)	It is independent of first-unit demand.
	ii)	It is negative monotonic; that is, u'(s) < 0.
	iii)	The integral of u(s) from zero to infinity is finite.
3)	First-unit demand conforms to proportionate effect:
	i)	Value changes each day by a proportion (called 1+j, with j denoting the day), of the previous day's value.
	ii)	In the long run, the j's may be considered random as they are not directly related to each other nor are they uniquely a function of value.
	iii)	The j's are taken from an unspecified distribution with a finite mean and a non-zero, finite variance (1999, pp. xxiii-xxiv).

Axiom #3 implies, by an easy proof, that the distribution of people's points of indifference for their first unit of a phenomenon relative to money, c₀(m), is lognormal; that is, the natural logarithm of the number of people who are indifferent at a particular price, m, is cumulatively (normally) distributed. The cumulative distribution is applicable to a variable that is subject to a process of change such that, at each step, a random quantity is added to the accumulated value of that variable. By the Central Limit Theorem, the distribution of the sum of a large number of independent, identically distributed random variables (from an unspecified distribution with a finite mean and a non-zero, finite variance) is approximately normal.

c₀(m), however, does not accumulate, rather it is analogous to the growth of the value of money through history: It conforms to the characteristics of proportionate effect. After the j'th day of a person's life, the change in the number of monetary units to which he is indifferent, relative to the first unit of a phenomenon, is a proportion of his indifference point the day before. That anthropometric variables (height, size of organs, tolerance to drugs, etc.) conform to the characteristics of proportionate effect is well established in the literature.

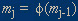
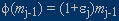
That first unit demand conforms to the characteristics of proportionate effect must be regarded as an axiom. A plausibility argument is provided here. Let with m_j the number of monetary units to which one is indifferent relative to the first unit of a phenomenon on the j'th day of that person's life. We want to show that Consider a man who wants to take out a loan at interest. He must think he will have more money in the future than he does now. 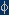(More money holdings, not necessarily more wealth.) If he does, the value of individual monetary units will tend to decrease over time relative to other phenomena; that is, is a positive function when averaged over all phenomena. To determine how much interest he is willing to pay, the man must specify this average . 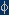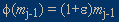For him to calculate the interest owed per unit of time as a percentage of the principle is equivalent to specifying with > 0 fixed. Fixing is a special case of _j being a random variable. Here, the probability density function is unity at and zero elsewhere.

Thus, the axiom that first unit demand conforms to the characteristics of proportionate effect is a generalization of calculating interest as a percentage of the amount owed. In fact, this is how people have calculated interest throughout recorded history, although economics having always been a soft science, they never asked for proof. Perhaps the value of money decays harmonically over time or in another way besides exponentially? This question is addressed in an appendix of my book but, for now, let us proceed to investigate the consequences of people's points of indifference for their first unit of each phenomenon being lognormally distributed. I believe that this axiom is on solid intuitive ground and will not be criticized. Even if it is, it is unlikely that critics will succeed in convincing the banking industry to calculate interest with a different formula, so the weight of tradition will continue to support my choice of the lognormal distribution for first unit demand.

Read my Simplified Exposition of Axiomatic Economics for a more detailed, but still undergraduate-level, discussion of my economic theory.  This paper requires knowledge of multi-variable calculus, but omits the real analysis that plagues readers of my 1999 book.

I also have an even easier non-mathematical explanation of the axioms, which is accessible to everybody.  Here, axiom #1 is compared to ordering children by height, but not to ordering them by intelligence.  Axiom #2 is shown to put some very mild restrictions on diminishing utility, a concept common to almost every school of economics.  Axiom #3 compares value to height, which is known to conform to proportionate effect.  Throughout one’s childhood, there are good days when one gets plenty to eat and there are bad days when one does not.  But the effect on one’s height is proportionate to what one has already obtained.  Big kids eat more on the good days than little kids because they have bigger stomachs.